Page 37 - E-Modul Kalkulus Integral
P. 37
e-Modul Kalkulus Integral
Program Studi Pendidikan Matematika
2.1 Integral Tentu
Integral tentu merupakan integral yang sudah memiliki batas-batas atau
sudah ditentukan batas bawah dan batas atasnya. Perhatikan Gambar 2.1
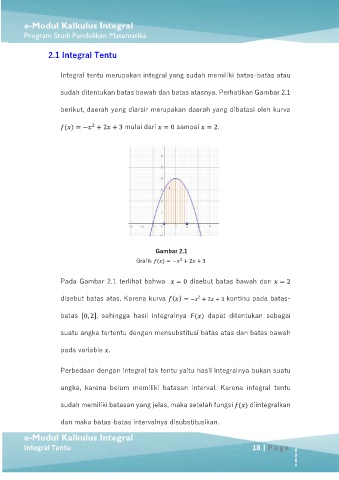
berikut, daerah yang diarsir merupakan daerah yang dibatasi oleh kurva
2
( ) = − + 2 + 3 mulai dari = 0 sampai = 2.
Gambar 2.1
2
Grafik ( ) = − + 2 + 3
Pada Gambar 2.1 terlihat bahwa = 0 disebut batas bawah dan = 2
disebut batas atas. Karena kurva ( ) = − + 2 + 3 kontinu pada batas-
2
batas [0, 2], sehingga hasil integralnya ( ) dapat ditentukan sebagai
suatu angka tertentu dengan mensubstitusi batas atas dan batas bawah
pada variable .
Perbedaan dengan integral tak tentu yaitu hasil integralnya bukan suatu
angka, karena belum memiliki batasan interval. Karena integral tentu
sudah memiliki batasan yang jelas, maka setelah fungsi ( ) diintegralkan
dan maka batas-batas intervalnya disubstitusikan.
e-Modul Kalkulus Integral
Integral Tentu 18 | P a g e