Page 14 - KIII GEOMETRIA 2DO SECUNDARIA

Geometría 2° Secundaria

17
SEMANA

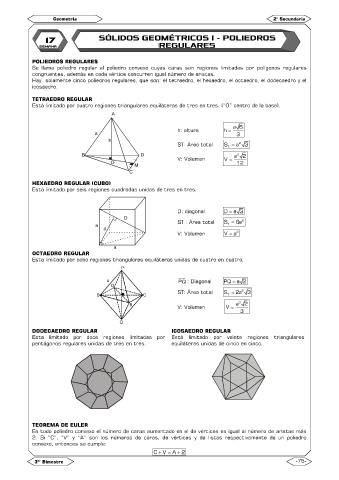
POLIEDROS REGULARES
Se llama poliedro regular al poliedro convexo cuyas caras son regiones limitadas por polígonos regulares
congruentes, además en cada vértice concurren igual número de aristas.
Hay solamente cinco poliedros regulares, que son: el tetraedro, el hexaedro, el octaedro, el dodecaedro y el
icosaedro.

TETRAEDRO REGULAR
Está limitado por cuatro regiones triangulares equiláteras de tres en tres. (“O” centro de la base).

a 6
h: altura h 
3
ST: Área total S  a 2 3
T
a 3 2
V: Volumen V 
12

HEXAEDRO REGULAR (CUBO)
Está limitado por seis regiones cuadradas unidas de tres en tres.

D: diagonal D  a 3
2
ST : Área total S  6a
T
V: Volumen V  a
3

OCTAEDRO REGULAR
Esta limitado por ocho regiones triangulares equiláteras unidas de cuatro en cuatro.

PQ : Diagonal PQ  a 2
ST: Área total S  2a 2 3
T
a 3 2
V: Volumen V 
3

DODECAEDRO REGULAR ICOSAEDRO REGULAR
Esta limitado por doce regiones limitadas por Está limitado por veinte regiones triangulares
pentágonos regulares unidas de tres en tres. equiláteras unidas de cinco en cinco.

TEOREMA DE EULER
En todo poliedro convexo el número de caras aumentado en el de vértices es igual al número de aristas más
2. Si “C”, “V” y “A” son los números de caras, de vértices y de listas respectivamente de un poliedro
convexo, entonces se cumple:


C V  A 2
er
3 Bimestre -75-