Page 16 - KIII GEOMETRIA 2DO SECUNDARIA

Geometría 2° Secundaria

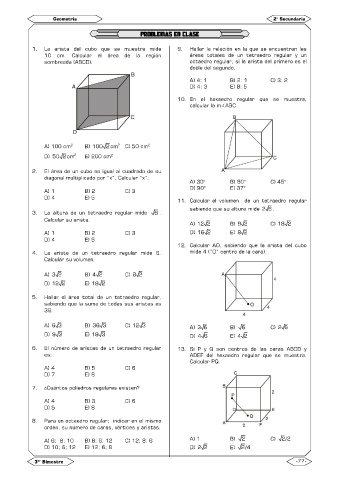
1. La arista del cubo que se muestra mide 9. Hallar la relación en la que se encuentran las
10 cm. Calcular el área de la región áreas totales de un tetraedro regular y un
sombreada (ABCD). octaedro regular, si la arista del primero es el
doble del segundo.

A) 4: 1 B) 2: 1 C) 3: 2
D) 4: 3 E) 8: 5

10. En el hexaedro regular que se muestra,
calcular la mABC.

2
2
2
A) 100 cm B) 100 2cm C) 50 cm
2
D) 50 2cm E) 200 cm
2

2. El área de un cubo es igual al cuadrado de su
diagonal multiplicado por “x”. Calcular “x”.
A) 30° B) 60° C) 45°
A) 1 B) 2 C) 3 D) 90° E) 37°

D) 4 E) 5 11. Calcular el volumen de un tetraedro regular

sabiendo que su altura mide 2 6 .
3. La altura de un tetraedro regular mide 6 .
Calcular su arista.
A) 12 2 B) 9 2 C) 18 2
A) 1 B) 2 C) 3 D) 16 2 E) 8 2
D) 4 E) 5
12. Calcular AO, sabiendo que la arista del cubo
4. La arista de un tetraedro regular mide 6. mide 4 (“O” centro de la cara).
Calcular su volumen.

A) 3 2 B) 4 2 C) 8 2
D) 12 2 E) 18 2

5. Hallar el área total de un tetraedro regular,
sabiendo que la suma de todas sus aristas es
36.

A) 6 3 B) 36 3 C) 12 3 A) 3 6 B) 6 C) 2 6
D) 9 3 E) 18 3 D) 4 6 E) 4 2

6. El número de aristas de un tetraedro regular 13. Si P y Q son centros de las caras ABCD y
es: ADEF del hexaedro regular que se muestra.
Calcular PQ.
A) 4 B) 5 C) 6
D) 7 E) 8

7. ¿Cuántos poliedros regulares existen?

A) 4 B) 3 C) 6
D) 5 E) 8

8. Para un octaedro regular; indicar en el mismo
orden, su número de caras, vértices y aristas.

A) 6; 8; 10 B) 8; 6; 12 C) 12; 8; 6 A) 1 B) 2 C) 2/2
D) 10; 6; 12 E) 12; 6; 8 D) 2 2 E) 2/4

er
3 Bimestre -77-