Page 2 - SM GEOMETRIA 5

Geometría 5° San Marcos

25
Semana

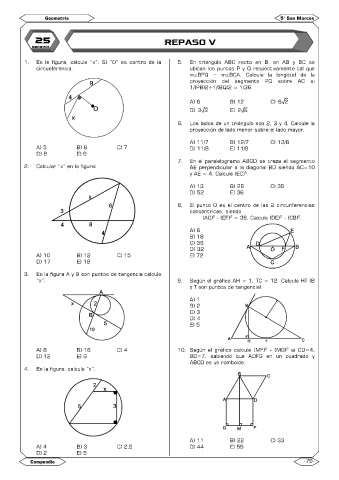
1. En la figura, calcule “x”. Si “O” es centro de ia 5. En triángulo ABC recto en B, en AB y BC se
circunferencia. ubican los puntos P y Q respectivamente tal que
m∠BPQ = m∠BCA. Calcule la longitud de la
proyección del segmento PQ sobre AC si
1/(PB)2+1/(BQ)2 = 1/36

A) 6 B) 12 C) 6 2
D) 3 3 E) 2 6

6. Los lados de un triángulo son 2, 3 y 4. Calcule la
proyección de lado menor sobre el lado mayor.

A) 11/7 B) 12/7 C) 13/8
A) 5 B) 6 C) 7 D) 11/8 E) 11/9
D) 8 E) 9
7. En el paralelogramo ABCD se traza el segmento
2. Calcular “x” en la figura: AE perpendicular a la diagonal BD siendo AC=10
y AE = 4. Calcule (EC) .
2

A) 13 B) 26 C) 39
D) 52 E) 36

8. El punto O es el centro de las 2 circunferencias
concéntricas, siendo
2
2
2
2
(AC) - (EF) = 36. Calcule (DE) - (CB) .

A) 6
B) 18
C) 36
D) 32
A) 10 B) 12 C) 15 E) 72
D) 17 E) 18

3. En la figura A y B son puntos de tangencia calcule
“x”. 9. Según el gráfico AH = 1, TC = 12. Calcule HT (B
y T son puntos de tangencia)

A) 1
B) 2
C) 3
D) 4
E) 5

2
2
A) 8 B) 16 C) 4 10. Según el gráfico calcule (MF) - (MG) si CD=4,
D) 12 E) 6 BD=7, sabiendo que ADFG en un cuadrado y
ABCD es un romboide.
4. En la figura, calcule “x”.

A) 11 B) 22 C) 33
A) 4 B) 3 C) 2,5 D) 44 E) 55
D) 2 E) 5
Compendio -79-