Page 6 - SM GEOMETRIA 5

Geometría 5° San Marcos

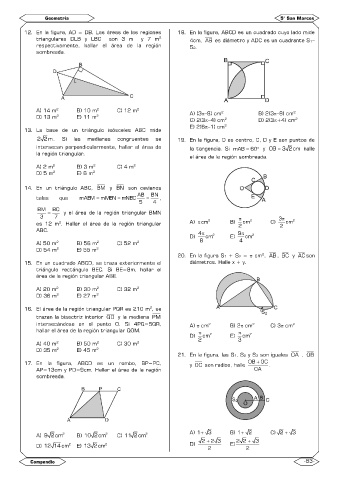
12. En la figura, AD = DB. Las áreas de las regiones 18. En la figura, ABCD es un cuadrado cuyo lado mide
2
triangulares DLB y LBC son 3 m y 7 m 4cm, AB es diámetro y ADC es un cuadrante S1–
respectivamente, hallar el área de la región S2.
sombreada.

2
2
2
A) 14 m B) 10 m C) 12 m A) (3–8) cm B) 2(3–8) cm
2
2
2
D) 13 m E) 11 m C) 2(3–4) cm D) 2(3+4) cm
2
2
2
2
13. La base de un triángulo isósceles ABC mide E) 2(6–1) cm

2 2m . Si las medianas congruentes se 19. En la figura, O es centro, C, D y E son puntos de
intersecan perpendicularmente, hallar el área de la tangencia. Si mAB = 60 y OB = 3 2cm halle

la región triangular. el área de la región sombreada.

2
2
2
A) 2 m B) 3 m C) 4 m
2
2
D) 5 m E) 6 m

14. En un triángulo ABC, BM y BN son cevianos
AB BN
tales que mABM = mMBN = mNBC = ,
5 4
BM = BC y el área de la región triangular BMN
3 7  3
2
2
2
es 12 m . Hallar el área de la región triangular A) cm 2 B) 2 cm C) 2 cm
ABC. 4 9
2
2
D) cm E) cm
2
2
2
A) 50 m B) 56 m C) 52 m 8 4
2
2
D) 54 m E) 55 m
2
20. En la figura S1 + S2 =  cm , AB , BC y AC son
15. En un cuadrado ABCD, se traza exteriormente el diámetros. Halle x + y.
triángulo rectángulo BEC. Si BE=8m, hallar el
área de la región triangular ABE.

2
2
2
A) 20 m B) 30 m C) 32 m
2
D) 36 m E) 27 m
2

16. El área de la región triangular PQR es 210 m , se
2
trazan la bisectriz interior QD y la mediana PM
intersecándose en el punto O. Si 4PQ=5QR, A)  cm B) 2 cm C) 3 cm
2
2
2
hallar el área de la región triangular QOM.  
2
2
D) 2 cm E) 3 cm
2
A) 40 m B) 50 m C) 30 m
2
2
2
2
D) 35 m E) 45 m
21. En la figura, las S1, S2 y S3 son iguales OA , OB
17. En la figura, ABCD es un rombo, BP=PC, y OC son radios, halle OB + OC .
AP=13cm y PD=9cm. Hallar el área de la región OA
sombreada.

2
2
2
A) 9 2cm B) 10 2cm C) 11 2cm A) 1+ 3 B) 1+ 2 C) 2 + 3
2 + 2 3 2 2 + 3
2
D) 12 14 cm E) 13 2cm D) 2 E) 2
2
Compendio -83-