Page 18 - KI - Trigonometría 4_Neat

Trigonometría 4° Secundaria

2 7. En un triángulo rectángulo ABC (B=90º) se
1. Se tiene “” agudo, además: Tg =
3 sabe que: a + b = 3c. Calcular:
Calcular: E = SenCos S = SecA + TgA

6 7 8 A) 1 B) 2 C) 3
A) B) C) D) 1/3 E) 6
13 13 13
9 13
D) E) 8. Del gráfico, calcular:
13 7 Ctg + Ctgβ

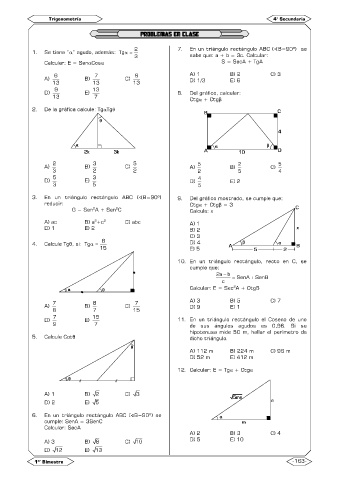
2. De la gráfica calcule: TgTg

2 3 5 5 2 5
A) B) C) A) B) C)
3 2 2 2 5 4
5 3 4
D) E) D) E) 2
3 5 5

3. En un triángulo rectángulo ABC (B=90º) 9. Del gráfico mostrado, se cumple que:
reducir: Ctg + Ctgβ = 3
G = Sen A + Sen C Calcule: x
2
2

2
2
A) ac B) a +c C) abc A) 1
D) 1 E) 2 B) 2
C) 3
8
4. Calcule Tgθ, si: Tg = D) 4
15 E) 5

10. En un triángulo rectángulo, recto en C, se
cumple que:
2a − b = SenA + SenB
c
Calcular: E = Sec A + CtgB
2

7 8 7 A) 3 B) 5 C) 7
A) B) C) D) 9 E) 1
8 7 15
7 15
D) E) 11. En un triángulo rectángulo el Coseno de uno
9 7 de sus ángulos agudos es 0,96. Si su
hipotenusa mide 50 m, hallar el perímetro de
5. Calcule Cotθ dicho triángulo.

A) 112 m B) 224 m C) 96 m
D) 52 m E) 412 m

12. Calcular: E = Tg + Ctg

A) 1 B) 2 C) 3
D) 2 E) 5

6. En un triángulo rectángulo ABC (∢B=90º) se
cumple: SenA = 3SenC
Calcular: SecA
A) 2 B) 3 C) 4
A) 3 B) 8 C) 10 D) 5 E) 10

D) 12 E) 13

er
1 Bimestre -163-