Page 131 - KM Matematika_BS_KLS_IX

Fungsi-Fungsi Muncul dalam Gambar

a
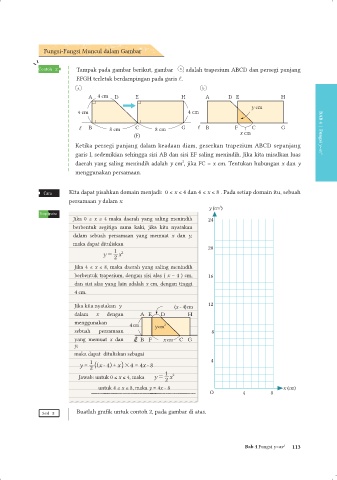
Contoh 2 Tampak pada gambar berikut, gambar , adalah trapesium ABCD dan persegi panjang
EFGH terletak berdampingan pada garis l.

a b
A 4 cm D E H A D E H
y cm
4 cm 4 cm

l B 8 cm C 8 cm G l B F C G
(F) x cm BAB 4 | Fungsi y=ax²
Ketika persegi panjang dalam keadaan diam, geserkan trapezium ABCD sepanjang
garis l, sedemikian sehingga sisi AB dan sisi EF saling menindih. Jika kita misalkan luas
daerah yang saling menindih adalah y cm , jika FC = x cm. Tentukan hubungan x dan y
2
menggunakan persamaan.

Cara Kita dapat pisahkan domain menjadi: 0 ≤ x ≤ 4 dan 4 ≤ x ≤ 8 . Pada setiap domain itu, sebuah
persamaan y dalam x.
y (cm )
2
Penyelesaian
Jika 0 ≤ x ≤ 4 maka daerah yang saling menindih 24
berbentuk segitiga sama kaki, jika kita nyatakan
dalam sebuah persamaan yang memuat x dan y,
maka dapat dituliskan 20
1 2
y = x
2
Jika 4 ≤ x ≤ 8, maka daerah yang saling menindih
berbentuk trapesium, dengan sisi alas ( x – 4 ) cm, 16
dan sisi alas yang lain adalah x cm, dengan tinggi
4 cm.

Jika kita nyatakan y (x - 4) cm 12
dalam x dengan A E D H
menggunakan 4 cm 2
sebuah persamaan y cm 8
yang memuat x dan B F x cm C G
y,
maka dapat dituliskan sebagai
1 4
y = ^ " x 4 + , 4 x 4 - 8
x # =
- h
2
Jawab: untuk 0 ≤ x ≤ 4, maka y = 1 x 2
2
untuk 4 ≤ x ≤ 8, maka y = 4x - 8 x (cm)
O 4 8

Soal 5 Buatlah grafik untuk contoh 2, pada gambar di atas.

Bab 4 Fungsi y=ax 2 113