Page 76 - u4

P1: OSO/OVY
GO01962-Smith-v1.cls
UAE-Math-Grade-12-Vol-1-SE-718383-ch4
CHAPTER 4 • •
Applications of Differentiation
266 P2: OSO/OVY QC: OSO/OVY T1: OSO October 25, 2018 17:24 4-56
EXAMPLE 6.6 Graphing the Sum of a Polynomial
and a Trigonometric Function
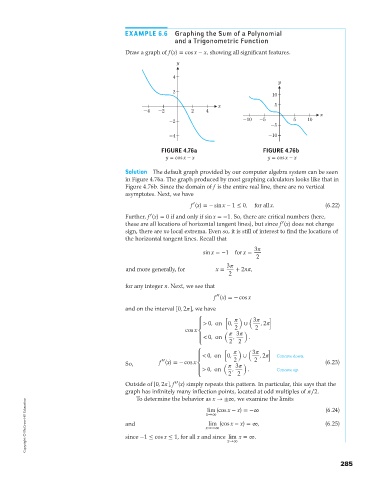
Draw a graph of f(x) = cos x − x, showing all significant features.
y

4
y
2
10
x 5
-4 -2 2 4
x
-2 -10 -5 5 10
-5
-4 -10

FIGURE 4.76a FIGURE 4.76b
y = cos x − x y = cos x − x
Solution The default graph provided by our computer algebra system can be seen
in Figure 4.76a. The graph produced by most graphing calculators looks like that in
Figure 4.76b. Since the domain of f is the entire real line, there are no vertical
asymptotes. Next, we have
′
f (x) = − sin x − 1 ≤ 0, for all x. (6.22)
′
Further, f (x) = 0 if and only if sin x =−1. So, there are critical numbers (here,
′
these are all locations of horizontal tangent lines), but since f (x) does not change
sign, there are no local extrema. Even so, it is still of interest to find the locations of
the horizontal tangent lines. Recall that

sin x =−1 for x = 3
2
and more generally, for x = 3 + 2n ,
2

for any integer n. Next, we see that
′′
f (x) = − cos x
and on the interval [0, 2 ], we have

[ ) ( 3 ]
> 0, on 0, ∪ , 2
⎧
cos x ⎪ 2 2
⎨ ( 3 )
⎪ < 0, on , .
2 2
⎩
[ ) ( 3 ]
< 0, on 0, ∪ , 2 Concave down.
⎧
2
′′
So, f (x) = − cos x ⎪ ( 3 ) 2 (6.23)
⎨
⎪ > 0, on , . Concave up.
⎩ 2 2
′′
Outside of [0, 2 ],f (x) simply repeats this pattern. In particular, this says that the
graph has infinitely many inflection points, located at odd multiples of ∕2.
To determine the behavior as x → ±∞, we examine the limits
Copyright © McGraw-Hill Education and x→∞ x→∞ (6.24)
lim (cos x − x) = −∞
(6.25)
lim (cos x − x) =∞,
x→−∞
since −1 ≤ cos x ≤ 1, for all x and since lim x =∞.

285