Page 20 - HS 9 Integraalrekening

GeoGebra in de derde graad

9.8 Hoofdstelling van de integraalrekening,
primitieve functie, (on)bepaalde integraal

9.8.1 Hoofdstelling van de integraalrekening

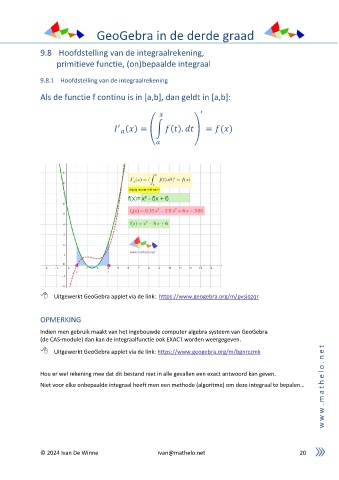
Als de functie f continu is in [a,b], dan geldt in [a,b]:

′

′
( ) = (∫ ( ). ) = ( )

 Uitgewerkt GeoGebra applet via de link: https://www.geogebra.org/m/pvsjqzqr

OPMERKING

Indien men gebruik maakt van het ingebouwde computer algebra systeem van GeoGebra
(de CAS-module) dan kan de integraalfunctie ook EXACT worden weergegeven.

t
 Uitgewerkt GeoGebra applet via de link: https://www.geogebra.org/m/bgnrczmk e
n
.
o
Hou er wel rekening mee dat dit bestand niet in alle gevallen een exact antwoord kan geven. l
e
Niet voor elke onbepaalde integraal heeft men een methode (algoritme) om deze integraal te bepalen… h
t
a

m
.
w
w
w

© 2024 Ivan De Winne ivan@mathelo.net 20