Page 25 - HS 9 Integraalrekening

GeoGebra in de derde graad

9.9.3 Geval 3: de gevraagde oppervlakte is gedeeltelijk gelegen
boven en ook onder de X-as

In dit geval moet men meerdere bepaalde integralen berekenen

Indien ∀ ∈ [ , ]; ( ) > 0

dan is de werkelijke oppervlakte S van dit gebied gelijk aan
1
de bepaalde integraal van f van a tot b

S 1 = ∫ ( ). > 0

1
Dit is meetkundig gezien de georiënteerde oppervlakte. S
Indien ∀ ∈ [ , ]; ( ) ≤ 0

dan is de werkelijke oppervlakte S van dit gebied gelijk aan
2
MIN de bepaalde integraal van f van a tot b

S - ∫ ( ). > 0
2 =

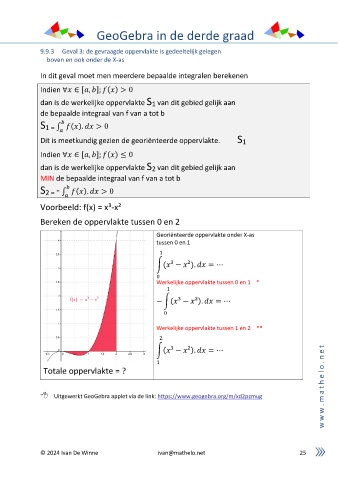
Voorbeeld: f(x) = x³-x²

Bereken de oppervlakte tussen 0 en 2

Georiënteerde oppervlakte onder X-as
tussen 0 en 1

1
∫( ³ − ²). = ⋯

0
Werkelijke oppervlakte tussen 0 en 1 *
1
− ∫( ³ − ²). = ⋯

0

Werkelijke oppervlakte tussen 1 en 2 **

2

∫( ³ − ²). = ⋯ t e
n
1 .
Totale oppervlakte = ? o l
e
h
t
a
 Uitgewerkt GeoGebra applet via de link: https://www.geogebra.org/m/xd2pzmug
m
.
w
w
w

© 2024 Ivan De Winne ivan@mathelo.net 25