Page 12 - HS 2 Combinatieleer

Combinatieleer, kansrekening en verklarende statistiek

Voorbeeld 3:

Bereken het aantal anagrammen van het woord RABARBER
Aantal letters n = 8

Aantal letters A is 2
Aantal letters B is 2
Aantal letters R is 3

Aantal letters E is 1
Totaal aantal mogelijke anagrammen van RABARBER is:

8! 8.7.6.5.4.3.2.1
̅
2,2,3..1 = = = 8.7.6.5 = 1680
8 2! 2! 3! 1! 2.1.2.1.3.2.1
Voorbeeld 4:
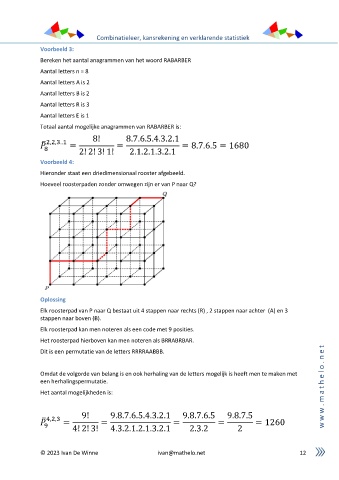
Hieronder staat een driedimensionaal rooster afgebeeld.

Hoeveel roosterpaden zonder omwegen zijn er van P naar Q?

Oplossing

Elk roosterpad van P naar Q bestaat uit 4 stappen naar rechts (R) , 2 stappen naar achter (A) en 3
stappen naar boven (B).

Elk roosterpad kan men noteren als een code met 9 posities.
Het roosterpad hierboven kan men noteren als BRRABRBAR.
t
Dit is een permutatie van de letters RRRRAABBB. e
n
.
o
Omdat de volgorde van belang is en ook herhaling van de letters mogelijk is heeft men te maken met l
e
een herhalingspermutatie. h
t
Het aantal mogelijkheden is: a
m
.
w
9! 9.8.7.6.5.4.3.2.1 9.8.7.6.5 9.8.7.5
̅
4,2,3 = = = = = 1260 w
9
4! 2! 3! 4.3.2.1.2.1.3.2.1 2.3.2 2 w

© 2023 Ivan De Winne ivan@mathelo.net 12