Page 4 - HS 6 Binomilae verdeling

Combinatieleer, kansrekening en verklarende statistiek

10 1 5 5 5
( = 5) = ( ) ∙ ( ) ∙ ( ) = 0,0130238102042
5 6 6
10 1 6 5 4
( = 6) = ( ) ∙ ( ) ∙ ( ) = 0,002170635034
6 6 6
10 1 7 5 3
( = 7) = ( ) ∙ ( ) ∙ ( ) = 0,0002480725753
7 6 6
10 1 8 5 2
( = 8) = ( ) ∙ ( ) ∙ ( ) = 0,0000186054431
8 6 6
10 1 9 5 1
( = 9) = ( ) ∙ ( ) ∙ ( ) = 0,0000008269086
9 6 6
10 1 10 5 0
( = 10) = ( ) ∙ ( ) ∙ ( ) = 0.0000000165382
10 6 6
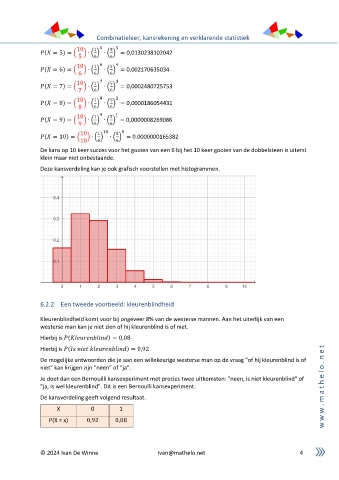
De kans op 10 keer succes voor het gooien van een 6 bij het 10 keer gooien van de dobbelsteen is uiterst
klein maar niet onbestaande.
Deze kansverdeling kan je ook grafisch voorstellen met histogrammen.

6.2.2 Een tweede voorbeeld: kleurenblindheid

Kleurenblindheid komt voor bij ongeveer 8% van de westerse mannen. Aan het uiterlijk van een
westerse man kan je niet zien of hij kleurenblind is of niet.

Hierbij is ( ) = 0,08

Hierbij is ( ) = 0,92 t
e
De mogelijke antwoorden die je aan een willekeurige westerse man op de vraag “of hij kleurenblind is of n
.
niet” kan krijgen zijn “neen” of “ja”. o
l
Je doet dan een Bernouilli kansexperiment met precies twee uitkomsten: "neen, is niet kleurenblind" of e
h
"ja, is wel kleurenblind". Dit is een Bernoulli kansexperiment. t
a
De kansverdeling geeft volgend resultaat. m
.
X 0 1 w

P(X = x) 0,92 0,08 w
w

© 2024 Ivan De Winne ivan@mathelo.net 4