Page 20 - HS 7 De normale verdeling

Combinatieleer, kansrekening en verklarende statistiek

7.7 Standaardisering van de normale kromme

7.7.1 Omvormen van normale verdeling naar de standaardnormale verdeling

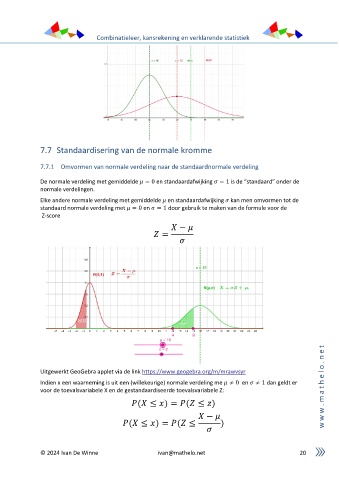
De normale verdeling met gemiddelde = 0 en standaardafwijking = 1 is de “standaard” onder de
normale verdelingen.
Elke andere normale verdeling met gemiddelde en standaardafwijking kan men omvormen tot de
standaard normale verdeling met = 0 en = 1 door gebruik te maken van de formule voor de
Z-score
−
=

t
e
n
.
o
Uitgewerkt GeoGebra applet via de link https://www.geogebra.org/m/mrawvsyr l
e
Indien x een waarneming is uit een (willekeurige) normale verdeling me ≠ 0 en ≠ 1 dan geldt er h
t
voor de toevalsvariabele X en de gestandaardiseerde toevalsvariabele Z: a
m
( ≤ ) = ( ≤ ) .
w
− w
( ≤ ) = ( ≤ ) w

© 2024 Ivan De Winne ivan@mathelo.net 20