Page 3 - HS 7 De normale verdeling
P. 3
Combinatieleer, kansrekening en verklarende statistiek
7.1.2 Absolute frequenties en histogram bij een verdeling in 25 klassen
Men kan de vorige meetresultaten ook indelen in 25 klassen, waarbij de klassenbreedte gelijk is aan 1.
In dit geval gaat er veel minder informatie verloren tegenover de indeling in slechts 5 klassen.
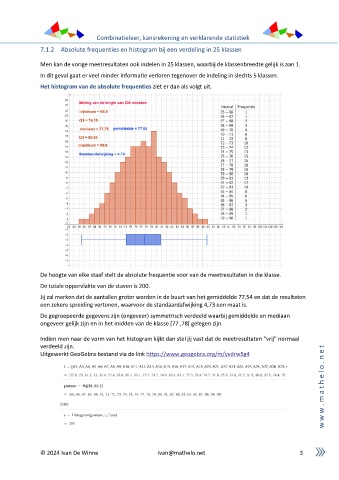
Het histogram van de absolute frequenties ziet er dan als volgt uit.
De hoogte van elke staaf stelt de absolute frequentie voor van de meetresultaten in die klasse.
De totale oppervlakte van de staven is 200.
Jij zal merken dat de aantallen groter worden in de buurt van het gemiddelde 77,54 en dat de resultaten
een zekere spreiding vertonen, waarvoor de standaardafwijking 4,73 een maat is.
De gegroepeerde gegevens zijn (ongeveer) symmetrisch verdeeld waarbij gemiddelde en mediaan
ongeveer gelijk zijn en in het midden van de klasse [77 ,78[ gelegen zijn.
Indien men naar de vorm van het histogram kijkt dan stel jij vast dat de meetresultaten “vrij” normaal
verdeeld zijn. t
Uitgewerkt GeoGebra bestand via de link https://www.geogebra.org/m/yvdrw5g4 e
n
.
o
l
e
h
t
a
m
.
w
w
w
© 2024 Ivan De Winne ivan@mathelo.net 3