Page 5 - HS 7 De normale verdeling

P. 5

Combinatieleer, kansrekening en verklarende statistiek

7.1.4 De normale kromme als wiskundig model voor een verdeling

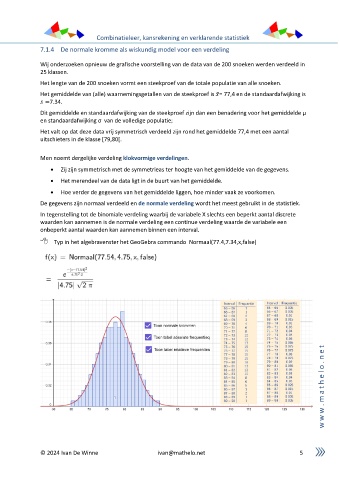
Wij onderzoeken opnieuw de grafische voorstelling van de data van de 200 snoeken werden verdeeld in
25 klassen.

Het lengte van de 200 snoeken vormt een steekproef van de totale populatie van alle snoeken.
̅
Het gemiddelde van (alle) waarnemingsgetallen van de steekproef is = 77,4 en de standaardafwijking is
=7.34.
Dit gemiddelde en standaardafwijking van de steekproef zijn dan een benadering voor het gemiddelde µ
en standaardafwijking σ van de volledige populatie;
Het valt op dat deze data vrij symmetrisch verdeeld zijn rond het gemiddelde 77,4 met een aantal
uitschieters in de klasse [79,80[.

Men noemt dergelijke verdeling klokvormige verdelingen.
• Zij zijn symmetrisch met de symmetrieas ter hoogte van het gemiddelde van de gegevens.

• Het merendeel van de data ligt in de buurt van het gemiddelde.

• Hoe verder de gegevens van het gemiddelde liggen, hoe minder vaak ze voorkomen.
De gegevens zijn normaal verdeeld en de normale verdeling wordt het meest gebruikt in de statistiek.
In tegenstelling tot de binomiale verdeling waarbij de variabele X slechts een beperkt aantal discrete
waarden kan aannemen is de normale verdeling een continue verdeling waarde de variabele een
onbeperkt aantal waarden kan aannemen binnen een interval.
 Typ in het algebravenster het GeoGebra commando Normaal(77.4,7.34,x,false)

t
e
n
.
o
l
e
h
t
a
m
.
w
w

1 2 3 4 5 6 7 8 9 10