Page 6 - HS 7 De normale verdeling
P. 6
Combinatieleer, kansrekening en verklarende statistiek
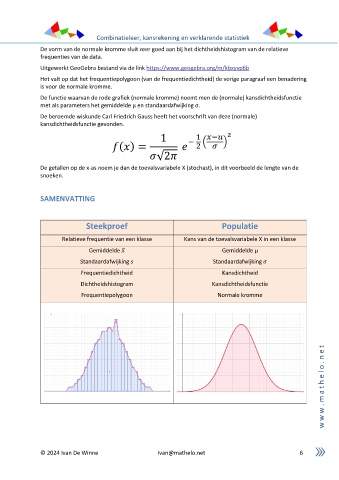
De vorm van de normale kromme sluit zeer goed aan bij het dichtheidshistogram van de relatieve
frequenties van de data.
Uitgewerkt GeoGebra bestand via de link https://www.geogebra.org/m/kbxyvp6b
Het valt op dat het frequentiepolygoon (van de frequentiedichtheid) de vorige paragraaf een benadering
is voor de normale kromme.
De functie waarvan de rode grafiek (normale kromme) noemt men de (normale) kansdichtheidsfunctie
met als parameters het gemiddelde µ en standaardafwijking σ.
De beroemde wiskunde Carl Friedrich Gauss heeft het voorschrift van deze (normale)
kansdichtheidsfunctie gevonden.
1 − ( ) 2
1 −
( ) = 2
√2
De getallen op de x-as noem je dan de toevalsvariabele X (stochast), in dit voorbeeld de lengte van de
snoeken.
SAMENVATTING
Steekproef Populatie
Relatieve frequentie van een klasse Kans van de toevalsvariabele X in een klasse
Gemiddelde ̅ Gemiddelde µ
Standaardafwijking Standaardafwijking
Frequentiedichtheid Kansdichtheid
Dichtheidshistogram Kansdichtheidsfunctie
Frequentiepolygoon Normale kromme
t
e
n
.
o
l
e
h
t
a
m
.
w
w
w
© 2024 Ivan De Winne ivan@mathelo.net 6