Page 5 - HS 8 Betrouwbaarheidsintervallen

Combinatieleer, kansrekening en verklarende statistiek

̅
Stap 4: neem van elke steekproef het gemiddelde .
Dit geeft een verzameling van 50 gemiddelden van de 50 steekproeven.

Stap 5: Bereken het gemiddelde van deze 50 gemiddelden van de 50 steekproeven.
Dit geeft 2,542 kg . Dit noemt men het steekproevengemiddelde.

Men kan ook de standaardafwijking van de 50 gemiddelden van de 50 steekproeven berekenen.
Dit geeft als standaardafwijking 0,018 gram.

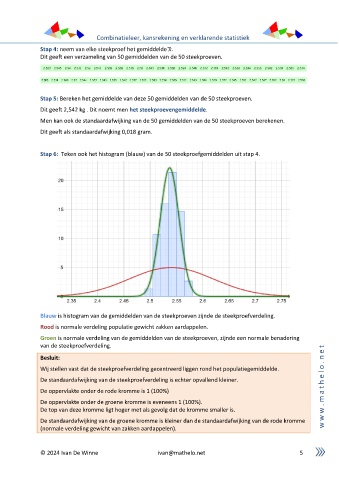
Stap 6: Teken ook het histogram (blauw) van de 50 steekproefgemiddelden uit stap 4.

Blauw is histogram van de gemiddelden van de steekproeven zijnde de steekproefverdeling.
Rood is normale verdeling populatie gewicht zakken aardappelen.

Groen is normale verdeling van de gemiddelden van de steekproeven, zijnde een normale benadering

van de steekproefverdeling. t
e
Besluit: n
.
Wij stellen vast dat de steekproefverdeling gecentreerd liggen rond het populatiegemiddelde. o
l
e
De standaardafwijking van de steekproefverdeling is echter opvallend kleiner.
h
t
De oppervlakte onder de rode kromme is 1 (100%) a
m
De oppervlakte onder de groene kromme is eveneens 1 (100%).
.
De top van deze kromme ligt hoger met als gevolg dat de kromme smaller is. w
De standaardafwijking van de groene kromme is kleiner dan de standaardafwijking van de rode kromme w
(normale verdeling gewicht van zakken aardappelen). w

© 2024 Ivan De Winne ivan@mathelo.net 5