Page 6 - HS 8 Betrouwbaarheidsintervallen

Combinatieleer, kansrekening en verklarende statistiek

De centrale limietstelling stelt dat de gemiddelden van steekproeven altijd normaal verdeeld
zullen zijn als je steekproeven van voldoende omvang neemt uit een populatie.
De steekproefgemiddelden vormen een steekproevenverdeling.

Wiskundigen hebben aangetoond dat een steekproevenverdeling zeer goed kan benaderd worden door
een normale verdeling indien het aantal elementen n van de steekproef voldoende groot is.

Het gemiddelde van de steekproefverdeling is bij benadering het gemiddelde van de populatie.
≅

De standaardafwijking van de steekproefverdeling is bij benadering de standaardafwijking van de
populatie, gedeeld door de vierkantswortel van de steekproefgrootte.

≅ (wortel-n wet)

√
µ = het gemiddelde van de populatie

σ = de standaardafwijking van de populatie
n = de steekproefgrootte (moet voldoende groot zijn n > 30).

Opmerking:
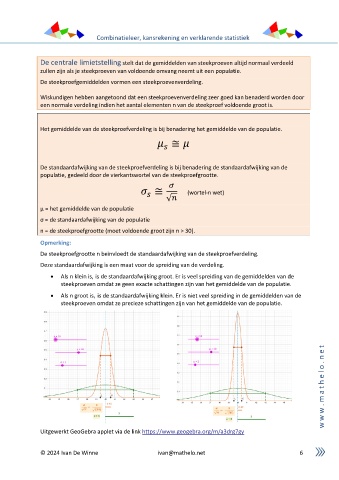
De steekproefgrootte n beïnvloedt de standaardafwijking van de steekproefverdeling.
Deze standaardafwijking is een maat voor de spreiding van de verdeling.

• Als n klein is, is de standaardafwijking groot. Er is veel spreiding van de gemiddelden van de
steekproeven omdat ze geen exacte schattingen zijn van het gemiddelde van de populatie.
• Als n groot is, is de standaardafwijking klein. Er is niet veel spreiding in de gemiddelden van de
steekproeven omdat ze precieze schattingen zijn van het gemiddelde van de populatie.

t
e
n
.
o
l
e
h
t
a
m
.
w

w
w
Uitgewerkt GeoGebra applet via de link https://www.geogebra.org/m/a3drg7gy

© 2024 Ivan De Winne ivan@mathelo.net 6