Page 87 - Mathematics 1
P. 87
مثال ( (3اُكت ْب عناص َر المجموعا ِت التالي ِة ُثَّم حّدد أياً منها مجموعة منتهية وأياً منها غير منتهي ٍة:
{ xعدد صحيح أكبرمن -3وأصغر من i) A ={ x : 3
} A = { -2 , -1 , 0 , 1 , 2 عدد عناصر المجموعة خمسة إذن هي مجموعٌة منتهيٌة
}ii) B ={ x ∈ Z : x > 6 xعدد صحيح أكبر من 6
لايمكن تحديد عدد عناصر المجموعة إذن هي مجموعة غير منتهية }… B ={ 7, 8 ,9 , 10 ,11 ,
مثال ( (4إذا كانت{ A={- 4, -3, -2,-1,0,1,2 ,3 ,4} , B = {-3, -1,0 ,2} , C= {-4, -2, 4, 6
بِيّ ْن هل أن كل من B ، Cمجموعة جزئية من المجموعة Aأم لا؟ مع ذكر السبب.
B⊆A Bمجموعة جزئية من Aلأن كل عنصر ينتمي الى Bينتمي الى A
C⊆A Cمجموعة غير جزئية من Aلأن العنصر 6ينتمي الى Cولاينتمي الى A
Operations On Sets [ ]4-1-3العمليا ُت على المجموعا ِت
مجموعة تقاطع المجموعتي ِن B , Aهي المجموع ُة التي عناص ُرها تنتمي إلى المجموع ِة Aوالمجموعة . B
ونعِبّ ُر عن مجموع ِة التقاط ِع كالآتيA ∩ B = { x : x ∈ A and x ∈ B} :
مجموعة اتحاد المجموعتين B , Aهي المجموعة التي عناصرها تنتمي إلى المجموعة Aأو المجموعة . B
وُنعِبّ ُر عن مجموع ِة الاتحاِد كالآتيA ∪ B = { x : x ∈ A or x ∈ B} :
مثال ( (5إذا كانت }A= {a, b , c , d ,e ,f ,g, h} , B = {b, d, e,f, k, m} , C= {a, g, h, n
i) A ∩ B ii) B ∩ C iii) B∩ A iv) B∪ C v) C∪B فأوجد:
}i) A∩ B = {a, b , c , d ,e ,f ,g, h} ∩{b, d, e,f, k, m} = {b , d , e , f
∅ = }ii) B ∩ C = {b, d, e,f, k, m} ∩{a, g, h, n
} iii) B ∩A = { b ,d ,e , f ُتسمى الإبدال لعملي ِة التقاط ِع A ∩ B = B ∩Aلاحظ أن
}iv) B ∪ C = {b, d, e,f, k, m} ∪ {a, g, h, n} = {b , d , e, f , k m ,a ,g ,h ,n
}v) C ∪ B = {b , d , e, f , k, m ,a ,g ,h ,n
لاح ْظ أن ُ B∪ C = C ∪ Bتسمى الإبدال لعملي ِة الاتحاِد
مثال ( (6إذاكانت }A= {-7 , -2 , 4, 6,7 ,8} , B = {-2, 1,4 , 8 ,9} , C= {-4, -2, 4,7, 9
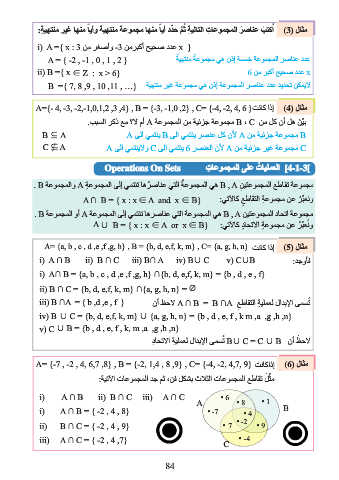
مِثّ ْل تقاطع المجموعات الثلاث بشكل فن ،ثم جد المجموعات الآتية:
i) A ∩ B ii) B ∩ C iii) A ∩ C A • 6 • 8 • 1 B
}i) A ∩ B = { -2 , 4 , 8 • -7 • 4
}ii) B ∩ C = { -2 , 4 , 9 • 7 • -2 • 9
}iii) A ∩ C = { -2 , 4 ,7 • -4
C
84