Page 7 - e-book Rotasi oleh Tri Ambarwati Nurul Putri

e-book Rotasi untuk kelas XI

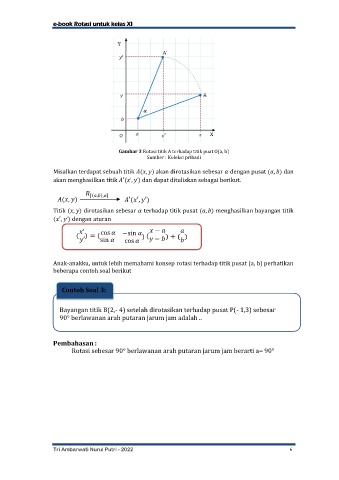
Gambar 3 Rotasi titik A terhadap titik puat O(a, b)
Sumber : Koleksi pribadi

Misalkan terdapat sebuah titik ( , ) akan dirotasikan sebesar dengan pusat ( , ) dan
akan menghasilkan titik ′( , ) dan dapat dituliskan sebagai berikut.
′
′

( , ) [( , ), ] ′( ′, ′)
Titik ( , ) dirotasikan sebesar terhadap titik pusat ( , ) menghasilkan bayangan titik
( ′, ) dengan aturan
′
′ cos −sin −
( ) = ( ) ( ) + ( )
′ sin cos −

Anak-anakku, untuk lebih memahami konsep rotasi terhadap titik pusat (a, b) perhatikan
beberapa contoh soal berikut

Contoh Soal 3:

Bayangan titik B(2,- 4) setelah dirotasikan terhadap pusat P(- 1,3) sebesar
90° berlawanan arah putaran jarum jam adalah ..

Pembahasan :
Rotasi sebesar 90° berlawanan arah putaran jarum jam berarti a= 90°

Tri Ambarwati Nurul Putri - 2022 6