Page 2 - PENGDEFINISIAN INTEGRAL (Magang Enggar MPMAT)
P. 2
1 1 1 1
‖ ‖ = {( − 0) , ( − ) , (1 − )}
3 2 3 2
1 1 1
‖ ‖ = {( ) , ( ) , ( )}
3 6 2
1
‖ ‖ =
2
1 1
3. = {0, , } bukan partisi karena titik ujung interval = 1 tidak termasuk
3
3
4 2
1 2 −1
4. = {0, , , … , , = 1} adalah partisi pada interval [a,b] dengan norma
4
1
‖ ‖ = karena setiap subintervalnya bernilai sama, maka partisi seperti ini disebut partisi seragam.
1
1
1 1
5. = {0, , , 1} bukan partisi sebab urutan 0 = < = < = < = 1 tidak terpenuhi.
3
2
0
5
1
3 4
4
3
Dengan kata lain bukan himpunan terurut sehingga bukan partisi.
5
B. Jumlahan Riemann
Diberikan interval [a,b] dan : [ , ] → ℝ fungsi bernilai rea yang terbatas pada [a,b].
Jika = { = , , , , … , = ; , , … , } partisi pada [a,b] . selanjutnya didefinisikan
1, 2
1
0
2
3
3
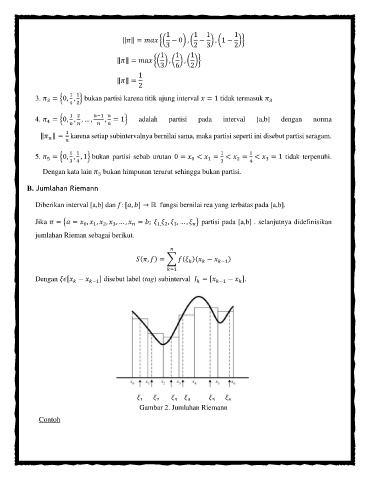
jumlahan Rieman sebagai berikut.
( , ) = ∑ ( )( − −1 )
=1
Dengan [ − −1 ] disebut label (tag) subinterval = [ −1 − ].
6
3
2
4
1
5
Gambar 2. Jumlahan Riemann
Contoh