Page 120 - Microeconomics, Fourth Edition

c03consumerpreferencesandtheconceptofutility.qxd 6/14/10 2:54 PM Page 94

94 CHAPTER 3 CONSUMER PREFERENCES AND THE CONCEPT OF UTILITY

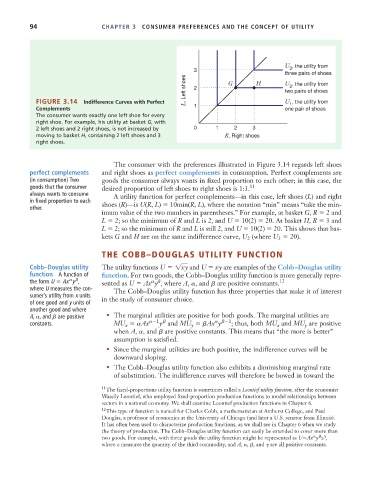
U , the utility from
3 3
three pairs of shoes
L, Left shoes 2 G H U , the utility from
2
two pairs of shoes
FIGURE 3.14 Indifference Curves with Perfect U , the utility from
1
Complements 1 one pair of shoes
The consumer wants exactly one left shoe for every
right shoe. For example, his utility at basket G, with
2 left shoes and 2 right shoes, is not increased by 0 1 2 3
moving to basket H, containing 2 left shoes and 3 R, Right shoes
right shoes.

The consumer with the preferences illustrated in Figure 3.14 regards left shoes
perfect complements and right shoes as perfect complements in consumption. Perfect complements are
(in consumption) Two goods the consumer always wants in fixed proportion to each other; in this case, the
goods that the consumer desired proportion of left shoes to right shoes is 1:1. 11
always wants to consume A utility function for perfect complements—in this case, left shoes (L) and right
in fixed proportion to each shoes (R)—is U(R, L) 10min(R, L), where the notation “min” means “take the min-
other.
imum value of the two numbers in parentheses.” For example, at basket G, R 2 and
L 2; so the minimum of R and L is 2, and U 10(2) 20. At basket H, R 3 and
L 2; so the minimum of R and L is still 2, and U 10(2) 20. This shows that bas-
kets G and H are on the same indifference curve, U 2 (where U 2 20).

THE COBB–DOUGLAS UTILITY FUNCTION

Cobb–Douglas utility The utility functions U 1xy and U xy are examples of the Cobb–Douglas utility
function A function of function. For two goods, the Cobb–Douglas utility function is more generally repre-

the form U Ax y , sented as U Ax y , where A, , and are positive constants. 12

where U measures the con- The Cobb–Douglas utility function has three properties that make it of interest
sumer’s utility from x units
of one good and y units of in the study of consumer choice.
another good and where
A, , and are positive • The marginal utilities are positive for both goods. The marginal utilities are
constants. MU x Ax 1 1 ; thus, both MU x and MU y are positive
y and MU y Ax y
when A, , and are positive constants. This means that “the more is better”
assumption is satisfied.
• Since the marginal utilities are both positive, the indifference curves will be
downward sloping.
• The Cobb–Douglas utility function also exhibits a diminishing marginal rate
of substitution. The indifference curves will therefore be bowed in toward the
11 The fixed-proportions utility function is sometimes called a Leontief utility function, after the economist
Wassily Leontief, who employed fixed-proportion production functions to model relationships between
sectors in a national economy. We shall examine Leontief production functions in Chapter 6.
12 This type of function is named for Charles Cobb, a mathematician at Amherst College, and Paul
Douglas, a professor of economics at the University of Chicago (and later a U.S. senator from Illinois).
It has often been used to characterize production functions, as we shall see in Chapter 6 when we study
the theory of production. The Cobb–Douglas utility function can easily be extended to cover more than

two goods. For example, with three goods the utility function might be represented as U Ax y z ,
where z measures the quantity of the third commodity, and A, , , and are all positive constants.