Page 121 - Microeconomics, Fourth Edition

c03consumerpreferencesandtheconceptofutility.qxd 6/14/10 2:55 PM Page 95

3.3 SPECIAL PREFERENCES 95

A

B
y U
3
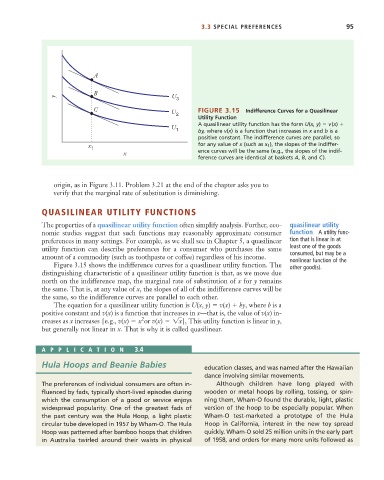
C U FIGURE 3.15 Indifference Curves for a Quasilinear
2
Utility Function
U A quasilinear utility function has the form U(x, y) v(x)
1 by, where v(x) is a function that increases in x and b is a
positive constant. The indifference curves are parallel, so
x for any value of x (such as x 1 ), the slopes of the indiffer-
1
x ence curves will be the same (e.g., the slopes of the indif-
ference curves are identical at baskets A, B, and C).

origin, as in Figure 3.11. Problem 3.21 at the end of the chapter asks you to
verify that the marginal rate of substitution is diminishing.

QUASILINEAR UTILITY FUNCTIONS

The properties of a quasilinear utility function often simplify analysis. Further, eco- quasilinear utility
nomic studies suggest that such functions may reasonably approximate consumer function A utility func-
preferences in many settings. For example, as we shall see in Chapter 5, a quasilinear tion that is linear in at
utility function can describe preferences for a consumer who purchases the same least one of the goods
amount of a commodity (such as toothpaste or coffee) regardless of his income. consumed, but may be a
nonlinear function of the
Figure 3.15 shows the indifference curves for a quasilinear utility function. The other good(s).
distinguishing characteristic of a quasilinear utility function is that, as we move due
north on the indifference map, the marginal rate of substitution of x for y remains
the same. That is, at any value of x, the slopes of all of the indifference curves will be
the same, so the indifference curves are parallel to each other.
The equation for a quasilinear utility function is U(x, y) v(x) by, where b is a
positive constant and v(x) is a function that increases in x—that is, the value of v(x) in-
2
creases as x increases [e.g., v(x) x or v(x) 1x]. This utility function is linear in y,
but generally not linear in x. That is why it is called quasilinear.

APPLICA TION 3.4

Hula Hoops and Beanie Babies education classes, and was named after the Hawaiian
dance involving similar movements.
The preferences of individual consumers are often in- Although children have long played with
fluenced by fads, typically short-lived episodes during wooden or metal hoops by rolling, tossing, or spin-
which the consumption of a good or service enjoys ning them, Wham-O found the durable, light, plastic
widespread popularity. One of the greatest fads of version of the hoop to be especially popular. When
the past century was the Hula Hoop, a light plastic Wham-O test-marketed a prototype of the Hula
circular tube developed in 1957 by Wham-O. The Hula Hoop in California, interest in the new toy spread
Hoop was patterned after bamboo hoops that children quickly. Wham-O sold 25 million units in the early part
in Australia twirled around their waists in physical of 1958, and orders for many more units followed as