Page 69 - Fiber Optic Communications Fund

50 Fiber Optic Communications

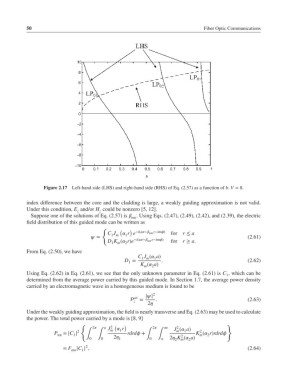
Figure 2.17 Left-hand side (LHS) and right-hand side (RHS) of Eq. (2.57) as a function of b. V = 8.

index difference between the core and the cladding is large, a weakly guiding approximation is not valid.
Under this condition, E and/or H could be nonzero [5, 12].
z
z
Suppose one of the solutions of Eq. (2.57) is . Using Eqs. (2.47), (2.49), (2.42), and (2.39), the electric
mn
field distribution of this guided mode can be written as
{
( ) −i(t− mn z−im)
C J r e for r ≤ a
1 m
1
= (2.61)
D K ( r)e −i(t− mn z−im) for r ≥ a.
1 m 2
From Eq. (2.50), we have
C J ( a)
1
1 m
D = . (2.62)
1
K ( a)
2
m
Using Eq. (2.62) in Eq. (2.61), we see that the only unknown parameter in Eq. (2.61) is C , which can be
1
determined from the average power carried by this guided mode. In Section 1.7, the average power density
carried by an electromagnetic wave in a homogeneous medium is found to be
2
 av = || . (2.63)
z
2
Under the weakly guiding approximation, the field is nearly transverse and Eq. (2.63) may be used to calculate
the power. The total power carried by a mode is [8, 9]
{ ( ) }
2 a J m 2 r 2 ∞ J ( a)
2
1
2
P 2 rdrd + m 1 K ( r)rdrd
tot = |C | ∫ ∫ ∫ ∫ 2 m 2
1
0 0 2 1 0 a 2 K ( a)
2
2 m
2
= F |C | , (2.64)
1
mn