Page 66 - Fiber Optic Communications Fund

Optical Fiber Transmission 47

1 10
J 0 (x)
0.8
J 1 (x) 0
0.6 J 2 (x)
0.4 J (x) Y 0 (x)
3
–10
0.2 Y (x)
1
J m 0 Y m –20 Y 2 (x)
–0.2
–30 Y 3 (x)
–0.4
–0.6
–40
–0.8
–1 –50
0 5 10 15 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
x x
(a) (b)

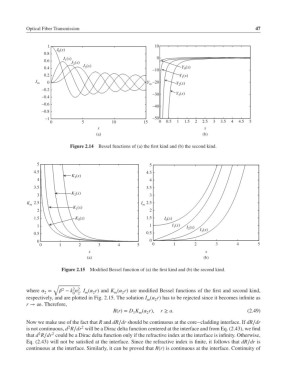
Figure 2.14 Bessel functions of (a) the first kind and (b) the second kind.

5 5
4.5 4.5
K 3 (x)
4 4
3.5 3.5
K (x)
3 2 3
2.5 I 2.5
K m m
K (x)
2 1 2
1.5 K 0 (x) 1.5 I 0 (x)
1 1 I (x) I (x)
1
2
I 3 (x)
0.5 0.5
0 0
0 1 2 3 4 5 0 1 2 3 4 5
x x
(a) (b)
Figure 2.15 Modified Bessel function of (a) the first kind and (b) the second kind.

√
2 2
2
where = − k n . I ( r) and K ( r) are modified Bessel functions of the first and second kind,
2 0 2 m 2 m 2
respectively, and are plotted in Fig. 2.15. The solution I ( r) has to be rejected since it becomes infinite as
m 2
r → ∞. Therefore,
R(r)= D K ( r), r ≥ a. (2.49)
1 m 2
Now we make use of the fact that R and dR∕dr should be continuous at the core–cladding interface. If dR∕dr
2
2
is not continuous, d R∕dr will be a Dirac delta function centered at the interface and from Eq. (2.43), we find
2
2
that d R∕dr could be a Dirac delta function only if the refractive index at the interface is infinity. Otherwise,
Eq. (2.43) will not be satisfied at the interface. Since the refractive index is finite, it follows that dR∕dr is
continuous at the interface. Similarly, it can be proved that R(r) is continuous at the interface. Continuity of