Page 23 - FINAL CFA II SLIDES JUNE 2019 DAY 9

LOS 34.k: Describe modern term structure READING 34: THE TERM STRUCTURE AND
models and how they are used. INTEREST RATE DYNAMICS
dr = a(b − r)dt + σdz MODULE 34.6: INTEREST RATE MODELS

Assume that the current short-term rate is r = 3% and the long-run value for the short-term rate is b = 8%. Also assume that the speed of the
adjustment factor is a = 0.40 and the annual volatility is σ = 2%. The Vasicek model provides the following formula for the change in short-
term interest rates, dr:

dr = 0.40(8% – r)dt + (2%)dz

The stochastic term, dz, is typically drawn from a standard normal distribution with a mean of zero and a standard deviation of 1. Assume
that a random number generator produced standard normal random error terms of 0.45, 0.18,−0.30, and 0.25.

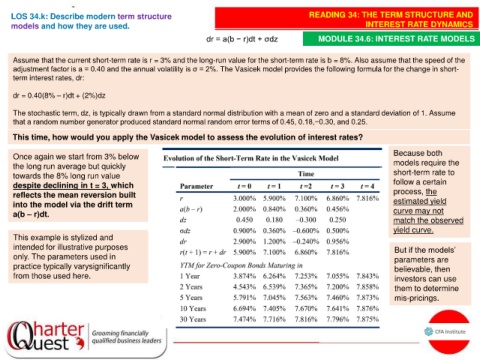
This time, how would you apply the Vasicek model to assess the evolution of interest rates?

Once again we start from 3% below Because both
the long run average but quickly models require the
towards the 8% long run value short-term rate to
despite declining in t = 3, which follow a certain
reflects the mean reversion built process, the
into the model via the drift term estimated yield
a(b – r)dt. curve may not
match the observed
yield curve.
This example is stylized and
intended for illustrative purposes But if the models’
only. The parameters used in parameters are
practice typically varysignificantly believable, then
from those used here. investors can use
them to determine
mis-pricings.