Page 245 - FUNDAMENTALS OF COMPUTER
P. 245
NPP
NPP Number System, Boolean Algebra and Logic Circuits 245
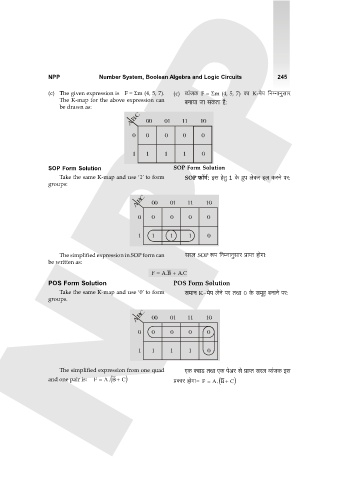
(c) The given expression is F = Σm (4, 5, 7). (c) ì`§OH$ F = Σm (4, 5, 7) H$m K-_on {ZåZmZwgma
The K-map for the above expression can ~Zm`m Om gH$Vm h¡:
be drawn as:
A B .C 00 01 11 10
0 0 0 0 0
1 1 1 1 0
SOP Form Solution SOP Form Solution
Take the same K-map and use ‘1’ to form SOP \$m°_©: Bg hoVw 1 Ho$ J«wn boH$a hb H$aZo na:
groups:
A B C 00 01 11 10
0 0 0 0 0
1 1 1 1 0
The simplified expression in SOP form can gab SOP ê$n {ZåZmZwgma àmßV hmoJm:
be written as:
F = B . A + C . A
POS Form Solution POS Form Solution
Take the same K-map and use ‘0’ to form g_mZ K-_on boZo na VWm 0 Ho$ g_yh ~ZmZo na:
groups.
A B C 00 01 11 10
0 0 0 0 0
1 1 1 1 0
The simplified expression from one quad EH$ ŠdmS> VWm EH$ noAa go àmßV gab ì`§OH$ Bg
and one pair is: F = A . (B + C ) àH$ma hmoJm- F = A . (B + C )