Page 89 - Modul problem posing berorientasi stem

4 Diperiksa Kembali langkah-langkah untuk pencarian 2

Memeriksa turunan ( ) = sinh → ( ) = cosh , maka ( ) =
kembali ( ). ′

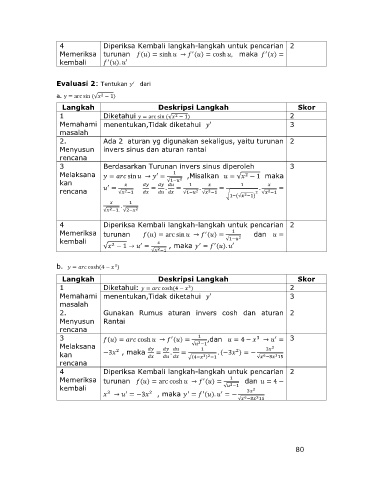
Evaluasi 2: Tentukan dari

a. y = arc sin (√ − 1)

Langkah Deskripsi Langkah Skor
1 Diketahui y = arc sin (√ − 1) 2

Memahami menentukan,Tidak diketahui ′ 3
masalah
2. Ada 2 aturan yg digunakan sekaligus, yaitu turunan 2
Menyusun invers sinus dan aturan rantai
rencana
3 Berdasarkan Turunan invers sinus diperoleh 3

Melaksana = sin → ′ = ,Misalkan = √ − 1 maka
kan
√
.
.
rencana = √ = = √ . √ = √ =

√
.

√ . √

4 Diperiksa Kembali langkah-langkah untuk pencarian 2

Memeriksa turunan ( ) = arc sin → ( ) = dan =
kembali √

√ − 1 → = , maka = ( ). ′

√

b. = cosh(4 − )

Langkah Deskripsi Langkah Skor
1 Diketahui: = cosh(4 − ) 2

Memahami menentukan,Tidak diketahui ′ 3
masalah
2. Gunakan Rumus aturan invers cosh dan aturan 2
Menyusun Rantai
rencana
3 ( ) = cosh → ( ) = ,dan = 4 − → = 3

Melaksana √

.
kan −3 , maka = = ( ) . (−3 ) = − √

rencana
4 Diperiksa Kembali langkah-langkah untuk pencarian 2

Memeriksa turunan ( ) = arc cosh → ( ) = dan = 4 −
kembali √

→ = −3 , maka = ( ). = −

√

80