Page 42 - SM Geometria 5to sec

Geometría 5° San Marcos

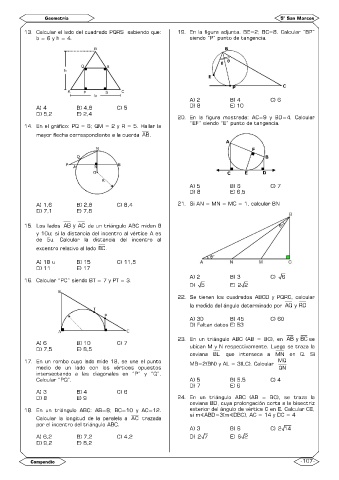
13. Calcular el lado del cuadrado PQRS sabiendo que: 19. En la figura adjunta. BE=2; BC=8. Calcular “BP”
b = 6 y h = 4. siendo “P” punto de tangencia.

A) 2 B) 4 C) 6
A) 4 B) 4,8 C) 5 D) 8 E) 10
D) 5,2 E) 2,4
20. En la figura mostrada: AC=9 y BD=4. Calcular
“EF” siendo “E” punto de tangencia.
14. En el gráfico: PQ = 6; QM = 2 y R = 5. Hallar la

mayor flecha correspondiente a la cuerda AB.

A) 5 B) 6 C) 7
D) 8 E) 6,5

A) 1,6 B) 2,8 C) 8,4 21. Si AN = MN = MC = 1, calcular BN
D) 7,1 E) 7,8

15. Los lados AB y AC de un triángulo ABC miden 8
y 10u; si la distancia del incentro al vértice A es
de 5u. Calcular la distancia del incentro al
excentro relativo al lado BC.

A) 18 u B) 15 C) 11,5
D) 11 E) 17
A) 2 B) 3 C) 6
16. Calcular “PC” siendo BT = 7 y PT = 3.
D) 5 E) 2 2

22. Se tienen los cuadrados ABCD y PQRC, calcular
la medida del ángulo determinado por AQ y RD

A) 30 B) 45 C) 60
D) Faltan datos E) 53

23. En un triángulo ABC (AB = BC), en AB y BC se
A) 6 B) 10 C) 7
D) 7,5 E) 8,5 ubican M y N respectivamente. Luego se traza la
ceviana BL que interseca a MN en Q. Si
17. En un rombo cuyo lado mide 18, se une el punto MB=2(BN) y AL = 3(LC). Calcular MQ
medio de un lado con los vértices opuestos QN
intersectando a las diagonales en “P” y “Q”.
Calcular “PQ”. A) 5 B) 5,5 C) 4
D) 7 E) 6
A) 3 B) 4 C) 6
D) 8 E) 9 24. En un triángulo ABC (AB = BC), se traza la
ceviana BD, cuya prolongación corta a la bisectriz
18. En un triángulo ABC: AB=8; BC=10 y AC=12. exterior del ángulo de vértice C en E. Calcular CE,
Calcular la longitud de la paralela a AC trazada si mABD=3(mDBC), AC = 14 y DC = 4
por el incentro del triángulo ABC.
A) 3 B) 6 C) 2 14
A) 6,2 B) 7,2 C) 4,2 D) 2 7 E) 6 2
D) 9,2 E) 8,2

Compendio -107-