Page 85 - E-MODUL- Aplikasi Turunan dengan Pendekatan RME Berbasis Pemecahan Masalah Polya

Tahap Melakukan Pengecekan 5

Jadi, mobil harus melaju pada ≈ 66.67

4 Pemecahan Masalah Polya 5

Tahap Memahami Masalah

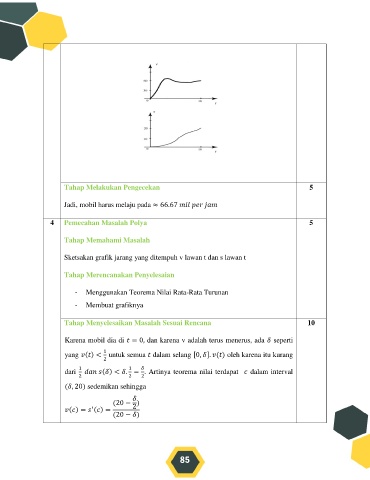
Sketsakan grafik jarang yang ditempuh v lawan t dan s lawan t

Tahap Merencanakan Penyelesaian

- Menggunakan Teorema Nilai Rata-Rata Turunan

- Membuat grafiknya

Tahap Menyelesaikan Masalah Sesuai Rencana 10

Karena mobil dia di = 0, dan karena v adalah terus menerus, ada seperti

1
yang ( ) < untuk semua dalam selang [0, ]. ( ) oleh karena itu kurang
2
1

1
dari ( ) < . = . Artinya teorema nilai terdapat dalam interval
2 2 2
( , 20) sedemikan sehingga

(20 − )
′
( ) = ( ) = 2
(20 − )

85