Page 147 - analysinew

147
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

● Μερικές από τις παραπά-
νω εκφράσεις στα ...
Μαθηματικά
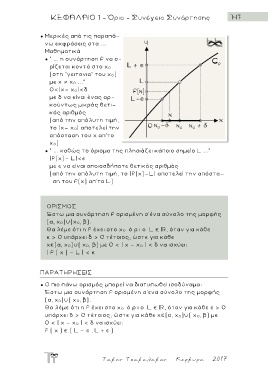
● " ... η συνάρτηση f να ο-

ρίζεται κοντά στο x 0
(στη "γειτονια" του x 0)
με χ x 0 ..."
0<|χ- x 0| < δ
με δ να είναι ένας αρ-
κ ο ύντως μικρός θετι-
κός αριθμός
(από την απόλυτη τιμή,
το |χ- x 0| α π οτελεί την
απόσταση του χ απ'το

x 0)
● " ... καθώς το όρισμα της πλησιάζει κάποιο σημείο L ..."
|f(χ)- L| < ε
με ε να είναι οποιοσδήποτε θετικός αριθμός
(από την απόλυτη τιμή, το |f(χ)-L| α π οτελεί την α π ό στα-
ση του f(χ) απ'το L)

ΟΡΙΣΜΟΣ
Έστω μια συνάρτηση f ορισμένη σ’ένα σύνολο της μορφής
(α, x 0) (x 0, β).
Θα λέμε ότι η f έχει στο x 0 ό ρ ι ο L , όταν για κάθε
ε > 0 υπάρχει δ > 0 τέτοιος, ώστε για κάθε
χ (α, x 0) ( x 0, β) με 0 < | x – x 0 | < δ να ισχύει:
| f ( x ) – L | < ε

ΠΑΡΑΤΗΡΗΣΕΙΣ

● Ο πιο πάνω ορισμός μπορεί να διατυπωθεί ισοδύναμα:
Έστω μια συνάρτηση f ορισμένη σ’ενα σύνολο της μορφής

(α, x 0) ( x 0, β).

Θα λέμε ότι η f έχει στο x 0 ό ρ ι ο L , όταν για κάθε ε > 0
υπάρχει δ > 0 τέτοιος, ώστε για κάθε χ (α, x 0) ( x 0, β) με

0 < | x – x 0 | < δ να ισχύει:

f ( x ) ( L – ε , L + ε )

Τακης Τσακαλακος Κερκυρα 2017