Page 288 - analysinew
P. 288
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
288
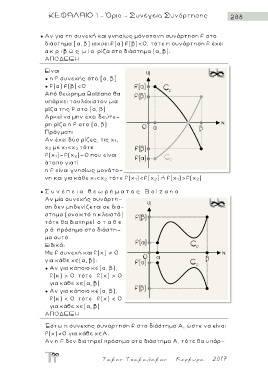
● Αν για τη συνεχή και γνησίως μόνοτονη συνάρτηση f στο
διάστημα [α, β] ισχύει f(α) f(β)<0, τότε η συνάρτηση f έχει
α κ ρ ι β ώ ς μ ί α ρίζα στο διάστημα (α, β).
ΑΠΟΔΕΙΞΗ
Είναι
● η f συνεχής στο [α, β]
● f(α) f(β)<0
Από θεώρημα Bolzano θ α
υπάρχει τουλάχιστον μια
ρίζα της f στο (α, β)
Αρκεί να μην έχει δεύτ ε -
ρη ρίζα η f στο (α, β)
Π ρ άγματι
Αν έχει δύο ρίζες, τις χ 1,
χ 2 με χ 1<χ 2 τότε
f(χ 1)=f( χ 2)=0 που είναι
άτοπο γιατί
η f είναι γνησίως μονότ ο -
νη και για κάθε χ 1<χ 2 τότε f(χ 1)<f(χ 2) ή f(χ 1)>f(χ 2)
● Σ υ ν έ π ε ι α θ ε ω ρ ή μ α τ ο ς B o l z a n o
Αν μία συνεχής συνάρτη-
σ η δεν μηδενίζεται σε διά-
στημα (ανοικτό η κλειστό)
τότε θα διατηρεί σ τ α θ ε
ρ ό π ρ όσημο στο διάστη-
μα αυτό
Ειδικά:
Με f συνεχή και f(x) 0
για κάθε x (α, β):
● Αν για κάποιο κ (α, β),
f(κ) > 0 τότε f(x) > 0
για κάθε x (α, β )
● Αν για κάποιο κ (α, β),
f(κ) < 0 τότε f(x) < 0
για κάθε x (α, β )
ΑΠΟΔΕΙΞΗ
Έστω η συνεχής συνάρτηση f στο διάστημα Α, ώστε να είναι
f(x) 0 για κάθε χ Α.
Αν η f δεν διατηρεί π ρ όσημο στο διάστημα Α, τότε θα υπά ρ -
Τακης Τσακαλακος Κερκυρα 2017