Page 286 - analysinew

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
286

ΠΡΟΤΑΣΗ
Έστω μια συνάρτηση f ορισμένη στο Α και χ 1 είναι ένα σημείο
του Α.
Αν η συνάρτηση f είναι συνεχής στο χ 1 Α και υπάρχει η
αντίστροφη της, τότε
η f - 1 είναι συνεχής στο χ 2 = f - 1 (χ 1) f(Α)

ΘΕΩΡΗΜΑΤΑ ΣΥΝΕΧΕΙΑΣ

ΘΕΩΡΗΜΑ BOLZANO

Aν μια συνάρτηση f, ορισμένη σ'ενα κλειστό διάστημα
[α, β] :
● είναι σ υ ν ε χ ή ς στο κλειστό διάστημα [α, β]

● ισχύει f ( α ) f ( β ) < 0
τότε υπάρχει έ ν α τ ο υ λ ά χ ι σ τ ο ν x 0 ∈ (α, β), τέτοιο
ώστε να ισχύει: f ( x 0 ) = 0 .

Δηλαδή υπάρχει τουλάχιστον μια ρίζα της εξίσωσης
f(x) = 0 στο ανοικτό διάστημα (α, β).

Ερμηνεία (Γεωμετρία )

Η γραφική παράσταση της

συνάρτησης f, που συνδέει
χ ω ρ ίς διακοπή
(προυπόθεση συνέχειας)

τα σημεία Α(α,f(α)) και

Β(β,f(β)) για τα οποία υπο-
θέτουμε ότι f(α) < 0 και

f(β) > 0 ή και αντίστροφα

(προυπόθεση f(α)∙f(β) < 0)
τ έ μ ν ε ι τ ο ν ά ξ ο ν α

x ’ x σ ’ έ ν α τ ο υ λ ά χ ι -
σ τ ο ν σ η μ ε ί ο x 0 του

διασ τ ήματος (α, β).

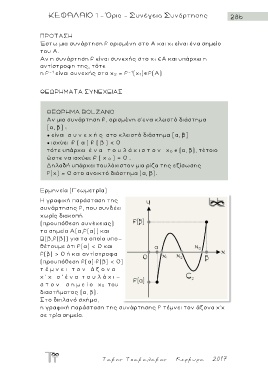
Στο διπλανό σχήμα,

η γραφική παράσταση της συνάρτησης f τέμνει τον άξονα χ'χ
σε τρία σημεία .

Τακης Τσακαλακος Κερκυρα 2017