Page 342 - analysinew

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
342

5. ΣΥΝΔΥΑΣΤΙΚΗ
Δίνεται η συνεχής συνάρτηση f στο (0,+ ) με
x <f(x)<χ +1 για κάθε χ>0
2
2
α) Να αποδείξετε οτι C f τέμνει την ευθεία y=2χ σε ένα
τουλάχιστον σημείο με τετμημένη χ 0 (0, 1)
β) Αν η συνάρτηση f είναι γνησίως αύξουσα να αποδείξετε
ότι
1 1
1) η συνάρτηση g(x)= f(x) + e x -1, x (0, + ) είναι γνη-
σίως φθίνουσα
2) η εξίσωση e +f(x)=e f(x) έχει μία μόνο λύση στο διά-
x
x

στημα (0, 2)

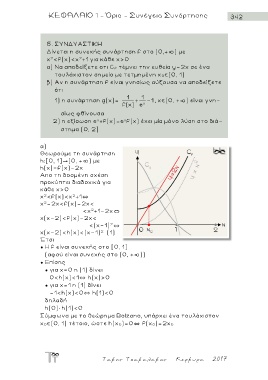
α )
Θεωρούμε τη συνάρτηση
h:[0, 1] (0, + ) με
h(x)=f(x)-2x
Aπο τη δοσμένη σχέση
προκύπτει διαδοχικά για
κάθε χ>0
2
x <f(x)<χ +1`
2
2
x -2χ<f(x)-2χ<
<χ +1-2χ`
2
χ ( x-2)<f(x)-2 χ <
<(χ-1) `
2
χ ( x-2)<h(x)<(χ-1) 2 (1)
Έτσι
● Η f είναι συνεχής στο [0, 1]

(αφού είναι συνεχής στο (0, + ))
● Επίσης
● για χ=0 η (1) δίνει
0<h(x)<1` h(x)>0
● για χ=1 η (1) δίνει
-1<h(x)<0` h(1)<0
δηλαδή
h(0) h(1)<0
Σύμφωνα με το θεώρημα Bolzano, υπάρχει ένα τουλάχιστον

χ 0 (0, 1) τέτοιο, ώστε h(χ 0)=0` f(χ 0)=2χ 0

Τακης Τσακαλακος Κερκυρα 2017