Page 338 - analysinew

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
338

3. ΣΥΝΔΥΑΣΤΙΚΗ
Δίνεται η συνάρτηση f με τύπο
f(x)=x 2 ν + 3 +αχ 2 ν + 1 -α 2 ν + 3 , χ , ν © και α>1
α) Να εξετάσετε ως προς τη μονοτονία τη συνάρτηση f

β) Να βρείτε το σύνολο τιμών της συνάρτησης f
γ) Να αποδείξετε ότι C f τέμνει μία μόνο φορά τον άξονα χ'χ
στο διάστημα (0, α)
δ) Να βρείτε το γεωμετρικό τόπο των σημείων Μ(α, β) αν
f(x)+α 2 3
lim ημ 2 1 =β, β
x 0

α )
Για κάθε x 1, x 2 με x 1 < x 2 ισχύει:
● x 1 < x 2 ~ x 1 2 ν + 3 < x 1 2 ν + 3
α > 0
● x 1 < x 2 ~ x 1 2 ν + 1 < x 1 2 ν + 1 ~ αx 1 2 ν + 1 < αx 1 2 ν + 1
Με πρόσθεση κατά μέλη
2 ν + 3 2 ν + 1 2 ν + 3 2 ν + 1 ~
x 1 + αx 1 < x 1 - αx 2
2 ν + 3 2 ν + 1 +α 2 ν + 3 2 ν + 3 2 ν + 1 -α 2 ν + 3 ~
x 1 +αx 1 < x 1 + αx 2
f(x 1) < f(x 2)
Άρα x 1 < x 2 ~ f(x 1) < f(x 2) που σημαίνει ότι η f είναι γνησίως
αύξουσα στο

β )
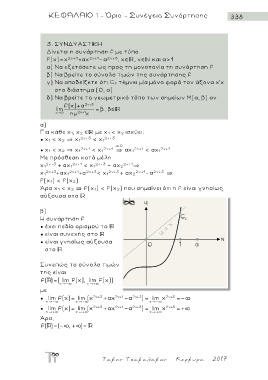
Η συνάρτηση f
● έχει πεδίο ορισμού το
● είναι συνεχής στο
● είναι γνησίως αύξουσα
στο

Συνεπώς το σύνολο τιμών
της είναι

f( )=( lim f(x) , lim f(x))
x - x +
με

● lim f(x) lim ( x 2ν+3 +αχ 2ν+1 -α 2ν+3 ) lim x 2ν+3
x - x - x -
● lim f(x) lim ( x 2ν+3 +αχ 2ν+1 -α 2ν+3 ) lim x 2ν+3
x + x + x +
Άρα,
f( )=( , )=

Τακης Τσακαλακος Κερκυρα 2017