Page 334 - analysinew

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
334

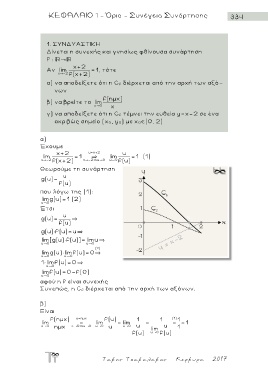
1. ΣΥΝΔΥΑΣΤΙΚΗ
Δίνεται η συνεχής και γνησίως φθίνουσα συνάρτηση
f :
x+2
Αν lim = 1, τότε
x - 2 f(x+2)
α) να αποδείξετε ότι η C f διέρχεται από την αρχή των αξό-
νων
f(ημx)
β) να βρείτε το lim x
x 0
γ) να αποδείξετε ότι η C f τέμνει την ευθεία y=χ-2 σε ένα
(0, 2)
ακριβώς σημείο (x 0, y 0) με χ 0

α )
Έχουμε
lim x+2 = 1 u = x + 2 lim u = 1 (1)
~
x - 2 f(x+2) x - 2 ~ u 0 u 0 f(u)
Θεωρούμε τη συνάρτηση
u
g(u)=
f(u)
που λόγω της (1):
limg(u)=1 (2)
u 0
Έτσι
u
g(u)= ~
f(u)
g(u) f(u)=u~
lim [g(u) f(u)]= limu~
u 0 u 0
(2 )
lim g(u) limf(u)= 0 ~
u 0 u 0
1 limf(u)=0~
u 0
limf(u)=0=f(0)
u 0
αφού η f είναι συνεχής
Συνεπώς, η C f διέρχεται από την αρχή των αξόνων.

β )
Είναι
f(ημx) u = ημx f(u) 1 1 (1) 1
lim = lim = lim = = = 1
x 0 ημx x 0 ~ u 0 u 0 u u 0 u lim u 1
f(u) u 0 f(u)

Τακης Τσακαλακος Κερκυρα 2017