Page 463 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 463

7.
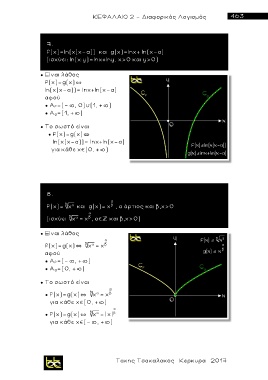
f(x)=ln(χ(x-α)) και g(x)=lnx+ ln(x-α)
(ισχύει: ln(x y)=lnx+lny, χ>0 και y>0)

● Είναι λάθος
f(x)=g(x)`
ln(χ(x-α))= lnx+ln(x-α )
αφού
● Α f=(- , 0) (1, + )
● Α g=(1, + )

● Tο σωστό είναι
● f(x)=g(x)`
ln(χ(x-α))= lnx+ln(x-α )
για κάθε χ (0, + )

8.
α
β
f(x)= χ και g(x)= χ , α άρτιος και β,χ>0
α
β
α
(ισχύει χ = χ , α και β,χ>0)
β
β
α

● Είναι λάθος
α
β
f(x)=g(x)` χ = χ
β
α
αφού
● Α f=(- , + )
● Α g=[0, + )

● Tο σωστό είναι
α
β
● f(x)=g(x)` χ = χ
α
β
για κάθε χ [0, + )
α
β
● f(x)=g(x)` χ = | χ|
β
α
για κάθε χ (- , + )

Τακης Τσακαλακος Κερκυρα 2017