Page 465 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 465

11.
Eστω η αντιστρεψιμη συνάρτηση

f:A και η f -1 : f(A)
Tα γραφήματα τους είναι συμμετρικά ως προς την ευθεία
y=x, που δεν είναι απαραίτητα μοναδική.

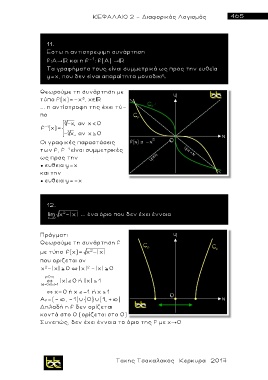
Θεωρούμε τη συνάρτηση με
τύπο f(x)=-x , x
3
... η αντίστροφη της έχει τύ-
πο
3 -χ , αν χ< 0
f (x)=
-1
- χ , αν χ 0
3
Οι γραφικές παρασ τ άσεις
των f, f - 1 είναι συμμετρικές

ως προς την
● ευθεια y=x
και την
● ευθεια y=-x

12.
lim χ -| χ| ... ένα όριο που δεν έχει έννοια
2
x 0

Πράγματι
Θεωρούμε τη συνάρτηση f

με τύπο f(x)= χ -| χ|
2
που οριζεται αν
2
2
χ -| χ| 0 ` | χ| -| χ| 0
ριζες
` | χ| 0 ή | χ| 1
|χ| =0 ή |χ|=1
` χ 0 ή χ 1 ή χ 1
Α f=(- , -1) {0} (1, + )
Δηλαδή η f δεν ορίζεται
κοντά στο 0 (ορίζεται στο 0)
Συνεπώς, δεν έχει έννοια το όριο της f με χ 0

Τακης Τσακαλακος Κερκυρα 2017