Page 460 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 460

1.
Δίνονται οι συναρτήσεις f(χ)=ημχ και g(χ)=συνχ, για κάθε
χ και
α) f(χ) + g(χ)= 0 ` ημχ + συνχ=0 ` ημχ =- συνχ (1)
β) f(χ) - g(χ)= 0 ` ημχ - συνχ=0 ` ημχ = συνχ (2)
και στις δύο περιπτωσεις, ισχύει ημχ 0 και συνχ 0

Πράγματι
Αν συνχ=0, τότε α π ό την
(1) ή (2) έχουμε και ημχ=0,
άτοπο αφού
ημ χ + συν χ=1`0=1,
2
2
που δεν ισχύει
Δηλαδή, δεν υπάρχει γωνία
φ ώστε τα ημφ και συνφ να
μηδενίζουν ταυτόχρονα.
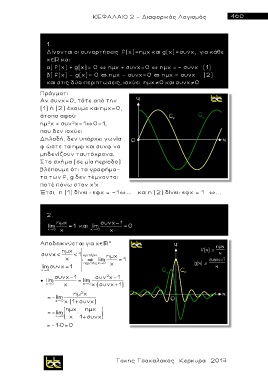
Στο σχήμα (σε μία περίοδο)
βλέπουμε ότι τα γ ρ αφήμα-
τα των f, g δεν τ έ μνονται
ποτέ πάνω στον x'x
Έτσι, η (1) δίνει : εφχ = -1`... και η (2) δίνει: εφχ = 1 `...

2.
ημχ 1 και lim συνχ-1 0
x lim χ x 0 χ
0

Αποδεικνύεται για χ *
ημχ
συνχ< < 1 κριτήριο ημχ
χ ~ lim = 1
limσυνχ 1 / ή x 0 χ
x 0
συνx 1 συν x-1
2
● lim lim
x 0 x x 0 x (συνx+1)
2
ημ x
=-lim
x 0 x (1+συνx)
ημx ημx
=-lim ×
x 0 x 1+συνx
=-1 0=0

Τακης Τσακαλακος Κερκυρα 2017