Page 5 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 5

Θ Ε Ω Ρ Ι Α ...

ΟΡΙΣΜΟΣ

Π α ρ ά γ ω γ ο ς σ ε σ η μ ε ί ο x 0
Έστω συνάρτηση f με πεδίο ορισμού Α και σημείο x 0 ∈ A.
Η f λέγεται π α ρ α γ ω γ ί σ ι μ η στο x 0, αν υπάρχει το όριο
f(x)-f(x )
lim 0 , και είναι πραγματικός αριθμός.
x
x
0 x-x
0
Το όριο αυτό λέγεται π α ρ ά γ ω γ ο ς της f στο x 0 και

συμβολίζεται f’ ( x 0).
Έτσι: f’ ( x 0) = lim f(x)-f(x )
0
x x 0 x-x 0
 Άλλος ορισμός: f’ (x 0) = lim f(x +h)-f(x )
0
0
h Ο h
(θέσαμε x = x 0 + h , οπότε h =x - x 0 και h 0).

Παράγωγος : ο παραγόμενος
α π ό το πρωτότυπο

(ετυμολογικά)

Η παράγωγος μίας συνάρτη-
σης με πραγματική μεταβλη-

τή είναι ένα μέτρο που εκ-

φράζει τη μεταβολή της τι-
μής της συνάρτησης

(μία συνάρτηση ή εξαρτημέ-

νη μεταβλητή - πρωτότυπο),
που προσδιορίζεται από μία

άλλη ποσότητα (ή ανεξάρ τ η -

τη μεταβλητή).

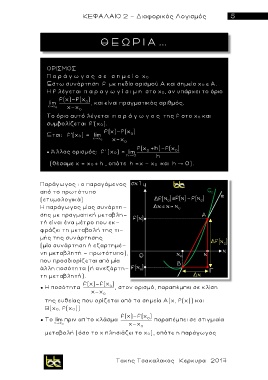
● Η ποσότητα f(x)-f(x ) , στον ορισμό, παραπέμπει σε κλίση
0
x-x
0
της ευθείας που ορίζεται από τα σημεία Α ( x, f(x)) και

Β(x 0, f(x 0))
f(x)-f(x )
● To lim πριν απ’το κλάσμα 0 παραπέμπει σε στιγμιαία

x
x
0 x-x 0

μεταβολή (όσο το χ πλησιάζει το x 0), οπότε η παράγωγος

Τακης Τσακαλακος Κερκυρα 2017