Page 9 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 9

df(x ) df(x)
● σύμφωνα με το Leibniz : 0 η
d d x= x 0

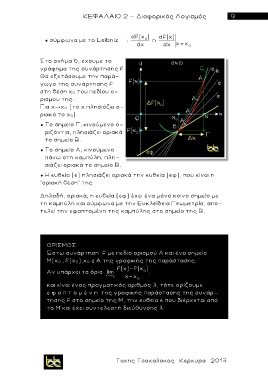
Στο σχήμα 6, έχουμε το
γ ρ άφημα της συνάρτησης f.
Θα εξετάσουμε την παρά-
γωγο της συνάρτησης f
στη θέση χ 0 του πεδίου ο-
ρισμου της.

Για χ χ 0 (το χ πλησιάζει ο-
ριακά το χ 0)

● Το σημείο Γ, κινούμενο ο-
ριζόντια, πλησιάζει οριακά
το σημείο Β.
● Το σημείο Α, κινούμενο

πάνω στη καμπύλη, πλη-
σ ι άζει οριακά το σημείο Β .

● Η ευθεία (ε) πλησιάζει οριακά την ευθεία (εφ), που είναι η
“οριακή θέση” της.

Δηλαδή, οριακά, η ευθεία (εφ) έχει ένα μόνο κοινο σημείο με
τη καμπύλη και σύμφωνα με την Ευκλείδεια Γεωμετρία , α π ο-

τελεί την εφαπτομένη της καμπύλης στο σημείο της Β.

ΟΡΙΣΜΟΣ
Έστω συνάρτηση f με πεδίο ορισμού Α και ένα σημείο
Μ ( x 0 , f(x 0),x 0 ∈ A της γραφικής της παράστασης.

0
Αν υπάρχει το όριο lim f(x)-f(x ) ,
x x 0 x-x
0
και είναι ένας πραγματικός αριθμός λ, τότε ορ ίζουμε
ε φ α π τ ο μ έ ν η της γραφικής παράστασης της συνάρ-
τησης f στο σημείο της Μ, την ευθεία ε που δι έρχεται από
το Μ και έχει συντελεστή διεύθυνσης λ.

Τακης Τσακαλακος Κερκυρα 2017