Page 12 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 12

Σ χ ό λ ι ο

● Αν υποθέσουμε ότι η σ υ -
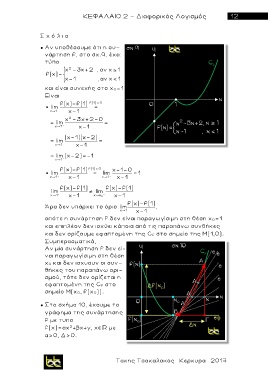
νάρτηση f, στο σχ.9, έχει
τύπο
χ 2 3x+2 , αν χ 1
f(x)=
x-1 , αν χ 1
και είναι συνεχής στο χ 0=1

Είναι
f(x)-f(1) f(1) 0
lim
x 1 x-1
x -3χ+2-0
2
= lim
x 1 x-1
(x-1)(χ-2)
lim
x 1 x-1

lim (χ-2)=-1
x 1
f(x)-f(1) f(1) 0 x-1-0
lim lim 1
x 1 x-1 x 1 x-1

f(x)-f(1) f(x)-f(1)
lim lim
x 1 x-1 x x 0 x-1
f(x)-f(1)
Άρα δεν υπάρχει το όριο lim ,
x 1 x-1
οπότε η συνάρτηση f δεν είναι παραγωγίσιμη στη θέση χ 0=1
και επιπλέον δεν ισχύει κάποια από τις παραπάνω συνθήκες
και δεν ορίζουμε εφαπτομένη της C f στο σημείο της Μ(1,0).
Συμπερασματικά,
Αν μία συνάρτηση f δεν ε ί -
ναι παραγωγίσιμη στη θέση
χ 0 και δεν ισχυουν οι συν-
θήκες του παραπάνω ορι-
σμού, τότε δεν ορίζεται η
εφαπτομένη της C f στο
σημείο M(x 0, f(χ 0)).

● Στο σχήμα 10, έχουμε το

γ ρ άφημα της συνάρτησης
f με τυπο
f(x)=αx +βχ+γ, χ με
2
α>0, Δ>0.

Τακης Τσακαλακος Κερκυρα 2017