Page 15 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 15

f(x)-f(0) f(0) 1 x+1-1
lim 1
x 0 x-0 x

lim f(x)-f(0) f(0) 1 -x+1-1 1
x 0 x-0 x
Άρα
f(x)-f(0) f(x)-f(0)
lim lim
x 0 x x 0 x
που σημαίνει ότι η συνάρτηση f δεν είναι παραγωγίσιμη στη
θέση χ 0=0.

● Αν μία συνάρτηση f δεν ε ί -
ναι συνεχής σε ένα σημείο
χ 0, τότε, σύμφωνα με το
παραπάνω θεώρημα δεν
μπορεί να είναι παραγωγίσι-
μη στο χ 0.
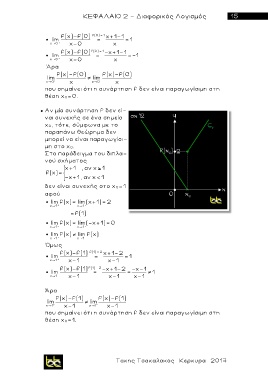
Στο παράδειγμα του διπλα-
ν ο ύ σχήματος
χ 1 , αν χ 1
f(x)=
-x+1 , αν χ 1
δεν είναι συνεχής στο χ 0=1

αφού
lim f(x)= lim(x+1)= 2
x 1 x 1
= f(1)

lim f(x)= lim(-x+1)= 0
x 1 x 1
lim f(x) lim f(x)
x 1 x 1
Όμως
f(x)-f(1) f(1) 2 x+1-2
lim 1
x 1 x-1 x-1

lim f(x)-f(1) f(1) 2 -x+1-2 -x-1 1
x 1 x-1 x-1 x-1

Άρα
f(x)-f(1) f(x)-f(1)
lim lim
x 1 x-1 x 1 x-1
που σημαίνει ότι η συνάρτηση f δεν είναι παραγωγίσιμη στη
θέση χ 0=1.

Τακης Τσακαλακος Κερκυρα 2017