Page 10 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 10

Σ χ ό λ ι α

● Η παράγωγος της παρα-
γωγίσιμης συνάρτησης f
στο χ 0, εκφράζει το συν-

τελεστή δ ι ε ύθυνσης (κλί-
ση) της εφαπτομένης (ε)
της C f στο σημείο
Μ ( χ 0, f(χ 0)).
Έτσι
● εφφ=λ=f’(χ 0)
● ε ξ ίσωση της εφαπτομέ-

ν η ς
y-f( χ 0) =f’(χ 0)(x-χ 0)
● η κλίση της εφαπτομέ-
νης (ε) της C f στο σ η -
μείο Μ ( χ 0, f(χ 0)), λέγεται και
● κ λ ίση της C f στο Μ
● κ λ ίση της f στο χ 0
f(x)-f(x )
● Στη περίπτωση που το όριο lim 0
x x 0 x-x 0
ισούται με + ή -
α ν άλογα
f(x)-f(x ) f(x)-f(x )
lim 0 =+ και lim 0 =- ή
x x 0 x-x x x 0 x-x
0 0
f(x)-f(x ) f(x)-f(x )
lim 0 =- και lim 0 =+
x x 0 x-x 0 x x 0 x-x 0
η συνεχής συνάρτηση f

δεν είναι παραγωγίσιμη,
αλλά έχει εφαπτομένη
την κατακόρυφη ευθεία
χ = χ 0.

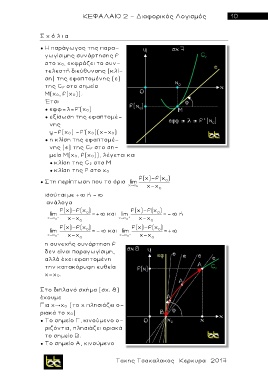
Στο διπλανό σχήμα (σχ. 8)

έχουμε
Για χ χ 0 (το χ πλησιάζει ο-
ριακά το χ 0)
● Το σημείο Γ, κινούμενο ο-
ριζόντια, πλησιάζει οριακά
το σημείο Β .
● Το σημείο Α, κινούμενο

Τακης Τσακαλακος Κερκυρα 2017