Page 7 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 7

f(x)-f(x )
lim 0
x x 0 x-x 180 0 f(x)-f(x ) f(x)-f(x )
0 lim x-x 0 lim x-x 0
lim f(x)-f(x ) x x 0 0 x x 0 0
0
x x 0 x-x
0
f(x)-f(x )
Άρα δεν υπάρχει το όριο lim 0 .
x x 0 x-x
0
Αν υποθέσουμε ότι η συνάρτηση f, στο σχ.3, έχει τύπο
f(x)=|x|+1, x και είναι συνεχής στο χ 0=0.
Ο τύπος γίνεται:
x+1 , αν χ 1
f(x)= και
-x+1, αν χ 1

f(x)-f(0) f(0) 1 x+1-1
lim lim 1
x 0 x-0 x 0 x
f(x)-f(0) f(0) 1 -x+1-1
lim lim 1
x 0 x-0 x 0 x
f(x)-f(0) f(x)-f(0)
lim lim
x 0 x x 0 x
f(x)-f(x )
Άρα δεν υπάρχει το όριο lim 0 .
x x 0 x-x 0

Η διαδικασία εύρεσης της
παραγώγου ονομάζεται
παραγώγιση.
Η παραγώγιση έχει εφαρμο-
γές σε όλες σχεδόν τις πο-

σοτ ι κές επιστήμες.
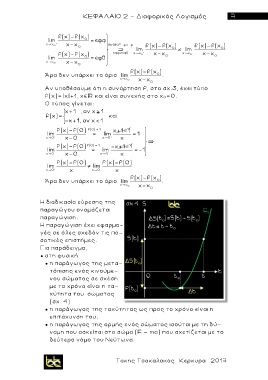
Για παράδειγμα,
● στη φυσική
● η παράγωγος της μετα-
τόπισης ε ν ός κινούμ ε -
νου σώματος σε σχέση
με το χρόν ο είναι η τα-
χύτητα του σώματος
(σχ. 4)

● η παράγωγος της ταχύτητας ως προς το χρόνο είναι η
επιτάχυνση του.
● η παράγωγος της ορμής ε ν ός σώματος ισ ο ύται με τη δύ-
ναμη που ασκείται στο σώμα (F = ma) που σχετίζεται με το
δ ε ύτερο νόμο του Ν ε ύτωνα.

Τακης Τσακαλακος Κερκυρα 2017