Page 6 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 6

περιγράφει την καλύτερη γραμμική προσέγγιση της συνάρ-
τησης κοντά στο x 0.
● Η ύπαρξη του ορίου εξασφαλίζει ότι το πρότύπο (συνάρτη-

σ η ) έχει την “ικανότητα” να παράγει, δηλαδή εξασφαλίζει την
ύπαρξη της παραγώγου, ενώ η τιμή της στη θέση x 0 είναι
πραγματικός αριθμός.
Σε αντίθετη περίπτωση, αν δεν υπάρχει το όριο η αν είναι ί σ ο
με + - , τότε η συνάρτηση δεν είναι παραγωγίσιμη.

.

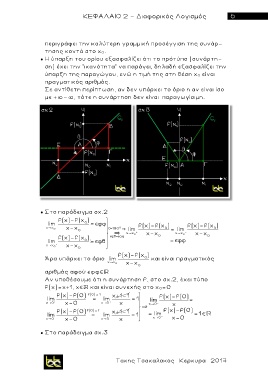
● Στο παράδειγμα σχ.2
f(x)-f(x )
lim 0 f(x)-f(x ) f(x)-f(x )
x x 0 x-x 180 0 lim 0 lim 0
0 ~ x x 0 x-x 0 x x 0 x-x 0
0
lim f(x)-f(x )
x x x-x
0 0
f(x)-f(x )
Άρα υπάρχει το όριο lim 0 και είναι πραγματικός
x x 0 x-x 0
αριθμός αφού εφφ
Αν υποθέσουμε ότι η συνάρτηση f, στο σχ.2, έχει τύπο
f(x)=x+1, x και είναι συνεχής στο χ 0=0

f(x)-f(0) f(0) 1 x+1-1 f(x)-f(0)
lim lim 1 lim =
x 0 x-0 x 0 x x 0 x
f(x)-f(0)
lim f(x)-f(0) f(0) 1 lim x+1-1 1 lim 1 §
x 0 x-0 x 0 x x 0 x-0

● Στο παράδειγμα σχ.3

Τακης Τσακαλακος Κερκυρα 2017