Page 14 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 14

ΘΕΩΡΗΜΑ
Αν η συνάρτηση f είναι π α ρ α γ ω ί σ ι μ η σε ένα σημείο
x 0, τότε είναι και σ υ ν ε χ ή ς στο σημείο αυτό.

ΑΠΟΔΕΙΞΗ
Για χ x 0 έχουμε
● f(x)-f(x ) f(x)-f(x ) (x-x )= + ή -
0
0 x-x 0 0
τότε
f(x)-f(x )
x lim[f(x)-f(x ) ] x lim x-x 0 (x-x )
0
0
x
x
0 0 0
f(x)-f(x )
x lim 0 x-x 0 0 x lim(x-x )
0
x
x
0
f παραγωγισιμη
f'(x ) 0 0
0
0
f'(x ) = lim 0 f(x) -f(x )
0
x -x
x
x
0
συνεπώς
lim[f(x)-f(x ) ] 0` lim f(x)- lim f(x ) 0` lim f(x) f(x )
x x 0 0 x x 0 x x 0 0 x x 0 0
που σημαίνει ότι η συνάρτηση f είναι συνεχής στο σημείο x 0 .

Σ χ ό λ ι ο
● Μία συνάρτηση f μπορεί να
είναι συνεχής σ’ένα σημείο
χ 0 χωρίς απαραίτητα να ε ί -
ναι και παραγωγίσιμη.
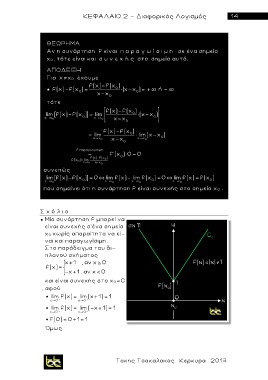
Στο παράδειγμα του δι-
πλανού σχήματος
χ 1 , αν χ 0
f(x)=
-x+1 , αν χ 0

και είναι συνεχής στο χ 0=0
, αφού
lim f(x)= lim (x+1)= 1
x 0 x 0
lim f(x)= lim (-x+1)= 1
x 0 x 0
f(0)= 0+1= 1

Όμως

Τακης Τσακαλακος Κερκυρα 2017