Page 97 - chapter 1

97
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

ΠΑΡΑΔΕΙΓΜΑΤΑ

1. MONOTONIA ΣΥΝΑΡΤΗΣΗΣ
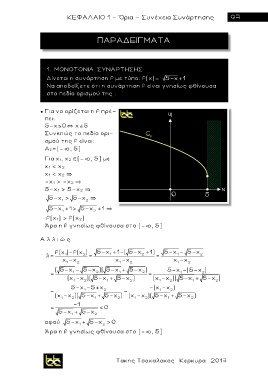
Δίνεται η συνάρτηση f με τύπο: f(x)= 5 x 1
Nα αποδείξετε ότι η συνάρτηση f είναι γνησίως φθίνουσα
στο πεδίο ορισμού της .

● Για να ορίζεται η f πρέ-
πει:
5-χ 0` χ 5
Συνεπώς το πεδίο ορι-
σμού της f είναι:
Α f=(- , 5]

Για x 1, x 2 (- , 5] με
x 1 < x 2
x 1 < x 2 ~
-x 1 > -x 2 ~
5-x 1 > 5-x 2 ~

5-x > 5-x ~
1
2

5-x +1> 5-x 2 1 ~
1
f(x 1) > f(x 2)
Άρα η f γνησίως φθίνουσα στο (- , 5]

Α λ λ ι ώ ς

f(x )-f(x ) 5-x +1-( 5-x +1) 5-x - 5-x
λ= 1 2 = 1 2 = 1 2
x -x 2 x -x 2 x -x 2
1
1
1
( 5-x - 5-x )( 5-x + 5-x ) 5-x -(5-x )
= 1 2 1 2 = 1 2
(x -x )( 5-x + 5-x ) (x -x )( 5-x + 5-x )
1 2 1 2 1 2 1 2
5-x -5+x -(x -x )
= 1 2 = 1 2
(x -x )( 5-x + 5-x ) (x -x )( 5-x + 5-x )
2
1
1
1
2
2
1
2
-1
= < 0
5-x + 5-x 2
1
αφού 5-x + 5-x >0
1 2
Άρα η f γνησίως φθίνουσα στο (- , 5]

Τακης Τσακαλακος Κερκυρα 2017