Page 94 - chapter 1

94
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

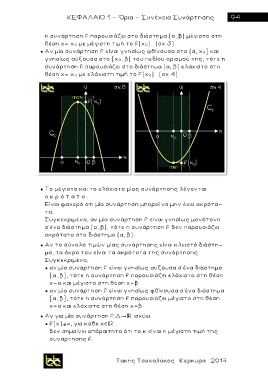
η συνάρτηση f παρουσιάζει στο διάστημα (α, β) μέγιστο στη
θέση χ= χ 0 με μέγιστη τι μ ή το f(χ 0) (σχ 3)
● Αν μία συνάρτηση f είναι γνησίως φθίνουσα στο (α, χ 0] και
γνησίως αύξουσα στο [χ 0, β) του πεδίου ορισμού της, τότε η

συνάρτηση f παρουσιάζει στο διάστημα (α, β) ελάχιστο στη
θέση χ= χ 0 με ελάχιστη τιμή το f(χ 0) (σχ 4)

● Τ ο μέγιστο και τ ο ελάχιστο μίας συνάρτησης λέγονται

α κ ρ ό τ α τ α .
Είναι φανερό οτι μία συνάρτηση μπορεί να μην έχει ακρότα-
τα.
Συγκεκριμένα, αν μία συνάρτηση f είναι γνησίως μονότονη
σ'ένα διάστημα (α, β), τότε η συνάρτηση f δεν παρουσιάζει
ακρότατα στο διάστημα (α, β).

● Α ν το σύνολο τιμών μίας συνάρτησης είναι κλειστό διάστη-
μα, τα άκρα του είναι τα ακρότατα της συνάρτησης.
Συγκεκριμένα,
● αν μία συνάρτηση f είναι γνησίως αύξουσα σ'ένα διάστημα
[α, β], τότε η συνάρτηση f παρουσιάζει ελάχιστο στη θέση
χ=α και μέγιστο στη θέση χ=β

● αν μία συνάρτηση f είναι γνησίως φθίνουσα σ ' ένα διάστημα
[α, β], τότε η συνάρτηση f παρουσιάζει μέγιστο στη θέση
χ=α και ελάχιστο στη θέση χ=β
● Αν για μία συνάρτηση f: Δ ισχύει

● f(x) κ, για κάθε χ
δεν σημαίνει απάραιτητα ότι το κ είναι η μέγιστη τιμή της
συνάρτησης f.

Τακης Τσακαλακος Κερκυρα 2017