Page 89 - chapter 1

89
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

πεδίου ορισμού, οπότε έχουν το ίδιο είδος μον ο τονίας και
στο διάστημα (a, x 0) (x 0, β) =(α, β)
(παράδειγμα g(x)= 0,7 - x , σχήμα)

● Aν η συνάρτηση f είναι γνησίως μονότονη σ'ένα διάστημα Δ
του πεδίου ορισμού της, τότε
η C f τέμνει τον άξονα χ'χ σε ένα το πολύ σημείο ή η εξίσωση
f(x)=0 έχει μία ρίζα στο Δ
ΑΠΟΔΕΙΞΗ

Έστω η C f τέμνει τον άξονα χ'χ σε δύο σημεία, τα χ 1, χ 2 με
χ 1<χ 2, συνεπώς f(χ 1)=0, f(χ 2)=0 και η f είναι γνησίως α ύ -
ξουσα (φθίνουσα) στο [χ 1, χ 2] Δ

Για x 0 (χ 1, χ 2) έχουμε
f
● x 0>χ 1 ~ f(x 0)> f(χ 1)~ f(x 0)>0
f
● x 0<χ 2 ~ f(x 0)< f(χ 2)~ f(x 0)<0
άτοπο, άρα η C f τέμνει τον άξονα χ'χ σε ένα το πολύ σημείο.

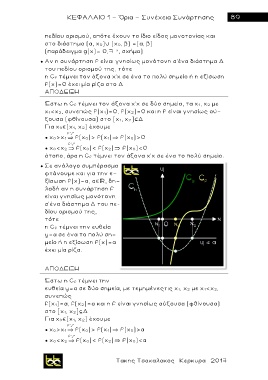
● Σε ανάλογο συμπέρασμα
φ τ άνουμε και για την ε-
ξίσωση f(x)=α, α , δη-
λαδή αν η συνάρτηση f
είναι γνησίως μονότονη

σ'ένα διάστημα Δ του π ε -
δίου ορισμού της,
τότε
η C f τέμνει την ευθεία
y=α σε ένα το πολύ ση-
μείο ή η εξίσωση f(x)=α
έχει μία ρίζα.

ΑΠΟΔΕΙΞΗ

Έστω η C f τέμνει την
ευθεία y=α σε δύο σημεία, με τεμημένεςτις χ 1, χ 2 με χ 1<χ 2,
συνεπώς
f(χ 1)=α, f(χ 2)=α και η f είναι γνησίως αύξουσα (φθίνουσα)
στο [χ 1, χ 2] Δ

Για x 0 (χ 1, χ 2) έχουμε
f
● x 0>χ 1 ~ f(x 0)> f(χ 1)~ f(x 0)>α
f
● x 0<χ 2 ~ f(x 0)< f(χ 2)~ f(x 0)<α

Τακης Τσακαλακος Κερκυρα 2017